Was gehört dazu? Welche Aufgaben kommen oft dran?
Bereitest du dich auf die Abiturklausur Vektorrechnung vor? Ich habe die IQB-Aufgaben für dich gesichtet und erzähle dir, was darin vorkam und wie du die Aufgaben angehst.
Meine Nachhilfeschüler:innen sind aktuell auf der Zielgeraden unter anderem in Mathematik. Und vielleicht betrifft dich das ja auch. Nachdem ich über die Abiturklausuren in Analysis und in Stochastik gebloggt habe, geht es in diesem Blogartikel um die Vektorrechnung.
Dieser Artikel ist zu deiner Information gedacht, aber auch als Abhakliste, was du schon sicher kannst. Und zur Planung, was du noch unbedingt wiederholen solltest. Ich habe Details und Tipps angefügt, die du durch Klick auf den jeweiligen Stichpunkt sichtbar machen kannst. Im Laufe der Zeit werde ich eventuelle neue Informationen noch ergänzen.
In Schleswig-Holstein werden die Abiturklausuren 2024 auf den IQB-Poolaufgaben basieren. Daher fokussiere ich mich mit dieser Artikelserie auf diese öffentlich einsehbaren Übungsaufgaben. Und zwar zunächst auf die Dokumente zum erhöhten Niveau aus den Jahren 2017 bis 2023.
Als Nächstes werde ich über die Aufgaben im hilfsmittelfreien Teil schreiben. Wenn ich damit fertig bin, füge ich Informationen über das grundlegende Niveau zu. Allerdings werden wenigstens in Schleswig-Holstein für 2024 Abiturklausuren auf grundlegendem Niveau noch dezentral gestellt. (Prüfungsregelungen als PDF)
Wichtig: Natürlich können in zukünftigen Klausuren Aufgaben vorkommen, die von meiner Liste nicht abgedeckt sind.
Dieser Blogartikel fasst alle meine Beiträge zur Vorbereitung auf das Matheabi zusammen:
Warum sind Klausuren vergangener Jahre interessant?
Viele Abituraufgaben im Fach Mathe wiederholen sich über die Jahre immer wieder. Das gilt auch für die Vektorrechnung. Daneben gibt es immer Knobelaufgaben aus dem Anforderungsbereich III, für die kreativ über den vorher eingeübten Lernstoff hinaus gedacht werden muss.
Wenn du die häufig vorkommenden Inhalte im Blick hast und diese bei deiner Vorbereitung gut übst, hat das zwei Vorteile:
- Du kannst diese Aufgaben schneller und zuverlässiger erledigen und hast dann mehr Zeit für die kniffeligeren Fragen.
- Du bist von vornherein entspannter. Das steigert deine Erfolgsaussichten ähnlich nachhaltig wie ein solides Faktenwissen.
Was ist mit Vektorrechnung gemeint?
Eigentlich heißt dieser Teilbereich der Oberstufenmathematik „lineare Algebra und analytische Geometrie“. Meiner Erfahrung nach können sich allerdings die meisten Menschen unter „Vektorrechnung“ mehr vorstellen und meine erste Priorität ist es, die Mathematik so verständlich und zugänglich wie möglich zu machen.
Es geht einerseits um Punkte, Flächen, Körper und Bewegungen im (üblicherweise) dreidimensionalen Raum. Andererseits gibt es noch den Teilbereich, der mit Matrizen Veränderungen zum Beispiel in Tierpopulationen, im Wahlverhalten oder in der Herstellung verschiedener Produkte aus unterschiedlichen Rohstoffen beschreibt.
Aufbau einer Abiturklausur Vektorrechnung
In ca. 80% der Fälle waren Sachaufgaben zu berechnen. Das liegt daran, dass sich auf die Realität bezogene Geschichten für eine Abiturklausur Vektorrechnung anbieten. Wie in der Analysis ist es aber auch möglich, dass in seltenen Fällen völlig kontextfrei ein Körper im Raum betrachtet wird.
In mehr als 80% der Klausuren gab es im Arbeitsblatt eine durchgehende Aufgabengrundgeschichte. Kugeln und Kreise kamen in den IQB-Aufgaben überhaupt nicht vor. Das könnte sich in Zukunft allerdings ändern.
Noch mehr als in der Analysis oder der Stochastik war oft eine Skizze zum Lösen einer Aufgabe sinnvoll bis notwendig. In vielen Fällen wurde eine solche Zeichnung sogar verlangt.
Sowohl bei Matrizen als bei geometrischen Aufgaben war Wissen aus der Mittelstufe und der Analysis gefordert:
Lineare Gleichungssysteme (Bestimmtheit, interpretieren, aufstellen)
In diesem Teil der Prüfung kannst du zum Lösen linearer Gleichungssysteme deinen Taschenrechner verwenden. Dafür solltest du vorher die Tastenfolgen einüben.
Damit dein Taschenrechner die Daten annehmen und korrekt verarbeiten kann, sind folgende Schritte wichtig:
Du musst die Gleichungen soweit „aufräumen“, dass alle Variablen auf der linken Seite und die Zahlen ohne Variablen rechts vom Gleichheitszeichen stehen.
Wenn es um Parameter r, s und t (oder andere Buchstaben 😉 ) geht, musst du im Blick haben, in welcher Reihenfolge diese in den linearen Gleichungen vorkommen. Denn der Taschenrechner bietet dir nur x, y und z an.
Hast du drei Gleichungen mit drei Variablen, kannst du unterschiedlich viele Lösungen bekommen. Bei einer Geraden und einer Ebene bedeutet zum Beispiel eine Lösung einen Schnittpunkt, keine Lösung, dass die Gerade parallel außerhalb der Ebene liegt und unendlich viele Lösungen, dass die Gerade in der Ebene verläuft.
Der Taschenrechner teilt dir mit, ob es unendlich viele Lösungen oder keine Lösungen gibt. Berechnest du ein Gleichungssystem von Hand, erkennst du unendliche viele Lösungen daran, dass deine Variablen immer wieder „verschwinden“ und Gleichungen der Sorte 5=5 übrig bleiben.
Es gibt keine Lösung, wenn die Variablen immer wieder heraus fallen und am Ende ein unmöglicher Ausdruck stehen bleibt, zum Beispiel 5=3.
Kommen in drei Gleichungen nur zwei Unbekannte vor, gibst du zwei Gleichungen in den Taschenrechner ein. Solltest du dabei zwei konkrete Werte für die jeweiligen Variablen erhalten, musst du diese noch in die dritte Gleichung einsetzen, um zu prüfen, dass sie auch gilt.
Bei Matrizen ergeben sich lineare Gleichungssysteme oft durch das Multiplizieren einer Matrix mit einem Vektor, wobei Elemente der Matrix oder des Vektors unbekannt sind. Im Prinzip kannst du diese Gleichungssysteme auch mit dem Taschenrechner lösen, meistens geht es aber nur um eine einzige Variable. In diesen Fällen ist der Zeitaufwand beim Lösen von Hand geringer als beim Eintippen in den Taschenrechner.
Anteil / Abweichung in Prozent
Es wurde relativ oft nach einer prozentualen Abweichung gefragt. Ich empfehle, das als Dreisatz zu sehen. Hier ein Beispiel:
| Länge | Prozent |
|---|---|
| 25 | 100 |
| 1 | 4 |
| 8 | 32 |
Wenn du dir diese Tabelle und diese Art zu rechnen merkst, musst du nur daran denken, dass du die Größe mit dem ganzen Wert in die erste Zeile schreibst, die abweichende in die dritte und eine 1 in die mittlere Zeile. Dann teilst du auf beiden Seiten durch den oberen Wert (hier: durch 25) und multiplizierst mit dem unteren Wert (hier: mal 8).
Dreisatztabellen sind außerdem auch eine gute Gedankenstütze für den hilfsmittelfreien Teil.
Definitionsmengen
Nicht nur in der Analysis können Zahlenbereiche vorgeschrieben sein. Wenn aus einer unendlich langen Geraden eine Strecke heraus geschnitten wird, zum Beispiel als Kante eines Körpers, dann darf der Geradenparameter nur eine bestimmte Menge an Werten annehmen.
Bei manchen Aufgaben wurde ein Parameter von Anfang an wie nebenbei eingeschränkt.
Beispiel:

Wenn sich am Ende der Rechnung dann mehrere Kandidaten für die richtige Antwort ergaben, mussten diejenigen ausgewählt werden, die in der Definitionsmenge waren. In diesem Fall sind nur positive reelle Zahlen zugelassen.
Es lohnt sich also, die Fragestellung noch einmal zu lesen, bevor du den Antwortsatz schreibst.
Die relevanten Zahlenmengen sind in der zugelassenen Formelsammlung aufgelistet. Daher musst du nicht auswendig lernen, wofür das R in der obigen Gleichung steht 😀
Grenzwerte
Grenzwertbetrachtungen kamen im Bereich der Matrizen vor. Bei einer Matrix mit zwei Parametern sollte einer davon gegen unendlich geführt werden.
So sah das Ganze aus:

Frage: „Für welche positiven Werte von a nähern sich alle Einträge mit k->∞ einem endlichen Wert?“
Manche Dinge, besonders in der Mathematik, sehen schlimmer aus, als sie sind. Ich empfehle immer, solche komplizierten Ausdrücke in kleine Bausteine aufzuteilen.
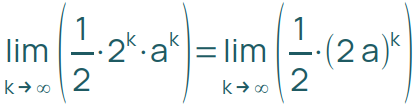
Damit dieser Grenzwert nicht ins Unendliche geht, muss 2a positiv aber kleiner oder gleich 1 sein. Und damit muss a kleiner oder gleich 0,5 sein.
Genauso geht (1-2kak) für ein positives a gegen -∞, wenn 2a größer als 1 ist.
Mein Tipp bei Grenzwerten, wie so oft: Atme durch. Dann stelle dir vor, was passiert, wenn du bei k einen Schieberegler hochziehst. Ein paar grundsätzliche Grenzwerte solltest du dir vor der Abiturklausur ansehen und verstehen. Hier ist eine Playlist von MathemaTrick zum Thema.
lineare Geradengleichungen aus der Analysis
In einer der Matrizenklausuren sollte die Abhängigkeit der benötigten Menge eines Rohstoffes von einem Parameter in einer Matrix ermittelt und in ein xy-Koordinatensystem gezeichnet werden.
Sei darauf vorbereitet, dass auch in der Abiturklausur Vektorrechnung Geradengleichungen wie in der Analysis vorkommen können.
| lineare Algebra | 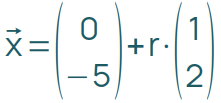 |
| Analysis | 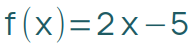 |
Parabeln erkennen und Scheitelpunkt finden
Es kam zweimal eine Geschichte vor, in der sich ein Ball auf einer Parabelbahn bewegte. Dafür war der Punkt gegeben, in dem sich der Ball zu einem bestimmten Zeitpunkt t befand:
P(32 − 8t / 5 / −5t 2 + 6,5t + 0,3)
Von der x-Koordinate werden für jede Sekunde 8 m abgezogen. Die y- Koordinate bleibt konstant auf 5. Die z-Koordinate (also die Höhe des Balls) hat die Form einer nach unten geöffneten Parabel.
Wie immer: Erstmal durchatmen. Der Arbeitsauftrag könnte lauten, wie hoch der Ball an der höchsten Stelle fliegt. Dafür musst du das Maximum der Parabel ausrechnen.
f(x) = −5t 2 + 6,5t + 0,3
f'(x) = -10t +6,5 f'(x) = 0 -> t = 0,65
f(0,65) = 2,1425
Der Ball kommt also auf eine Höhe von maximal 2,1425 m
Wenn gefragt ist, wo der Ball den Boden berührt, setzt du die z-Koordinate gleich null und löst die Gleichung nach t auf. Nur eine positive Zeit ist im Sachzusammenhang sinnvoll, weil der Ball ja nicht in die Vergangenheit fliegt. Und dieses t setzt du noch bei der x-Koordinate ein:
−5t 2 + 6,5t + 0,3 = 0 -> t1 = 1,34 und t2 = -0,04
32 – 8 · 1,34 =21,28 -> P(21,28 / 5 / 0)
Wichtig beim Lösen dieser Art Aufgaben ist, dass du verstanden hast, wie die drei Koordinaten als Ortsangabe im Raum gemeint sind. Und dass jede davon als eine Funktion formuliert sein kann, die mit den Mitteln der Analysis bearbeitet wird.
Pythagoras
Es sollte nicht überraschen, dass in einer Klausur über Geometrie sehr oft rechtwinklige Dreiecke auftauchen. Wenn die Länge einer Strecke gesucht ist, versuche es immer zuerst mit der Suche nach einem rechten Winkel und danach, ob unter zwei Katheten und einer Hypothenuse zwei der Seiten gegeben sind.
Sinus und Kosinus
Den Kosinus brauchst du, um Hilfe des Skalarproduktes Winkel zu berechnen. Die Formelsammlung enthält im Bereich Vektorrechung kaum Informationen, aber diese Formel steht darin 🙂
Wenn Winkel gegeben sind, kannst du mit dem Sinus oder dem Cosinus Strecken in einer Figur oder einem Körper berechnen.
Außerdem kommen sin und cos immer wieder in Aufgaben vor, in denen Terme interpretiert werden sollen. Eine Skizze hilft dabei sehr, wie fast immer 😉
Themenbereich Geometrie
Für mich ist diese Art Mathematik besonders faszinierend. Mit relativ einfachen rechnerischen Mitteln kann ich Dinge „herbei zaubern“, bewegen und miteinander in Kontakt treten lassen. Die Sachaufgaben sind im Grunde anschaulich und wiederholen oft sehr ähnliche Geschichten aus dem Alltag, zum Beispiel Sportplätze, Ballspiele, Gartenlauben oder Schattenwürfe. Wer ein einigermaßen gutes dreidimensionales Vorstellungsvermögen hat (und rechtzeitig übt, Skizzen zu zeichnen), kann die grundlegenden Aufgaben solide bewältigen.
Auf der anderen Seite wird für eine gute bis sehr gute Note erwartet, dass du nicht nur gewohnte Rechenvorgänge kennst, sondern die gelernten Konzepte kreativ und manchmal um die Ecke gedacht anwenden kannst. Mehr noch als in der Analysis und der Stochastik ist es für die Abiturklausur Vektorrechnung wichtig, dass du die grundlegenden Konzepte verstanden hast:
- Raum- und Symmetrieverständnis
- Punkte im Raum
- Geraden/Ebenen
- Flächen/Körper
- Winkel
- Beschreibungen von Bewegungen
Raum- und Symmetrieverständnis
Mit Hilfe der Symmetrie argumentieren
Oft heißt es in der Aufgabenstellung
„Geben Sie ohne weitere Berechnung einen Normalenvektor der Ebene an“
oder
„Begründen Sie, warum der Punkt P die gegebenen Koordinaten hat“
In den meisten Fällen geht es darum, dass etwas symmetrisch ist, und zwar an einer Ebene oder eine Achse gespiegelt oder um eine Achse gedreht. Oft ist das auch in der begleitenden Abbildung zu erkennen.
Für diese Art Aufgaben ist es wichtig, dass du Dinge im Kopf drehen und spiegeln kannst. Außerdem musst du verstanden haben, wie Orts- und Richtungsvektoren funktionieren.
Terme geometrisch interpretieren
Ich habe dazu Aufgaben von sehr unterschiedlicher Schwierigkeit gefunden.
Teils musst du einer Geradengleichung eine Kante eines Körpers oder eine Bewegung eines Objektes zuordnen.
In anderen Fällen war die Rechnung zu einer Art Lotfußpunktverfahren gegeben, mit deren Hilfe die neuen Koordinaten einer Ecke eines Körpers nach einer Drehung im Raum berechnet werden konnten.
Als Ansatz gehe ich immer mental die verschiedenen vektoriellen Rechenverfahren durch und überlege, bei welchem Verfahren ich zu einem ähnlichen Term komme. Das Schneiden von Geraden oder Ebenen und das Lotfußpunktverfahren kommen häufig vor.
Ein Beispiel aus einer Klausur von 2023, die Aufgabe war:
„Erläutern sie die Fragestellung, die zu diesen Gleichungen führte!“

Die erste Zeile hat das Format einer Ebenengleichung in der Normalenform. Der Vektor (6/-3/0) ist der Normalenvektor, (3/0/0) ist der Stützvektor dieser Ebene.
In der eckigen Klammer ist eine Gerade in der Parameterform eingesetzt worden. Der Stützvektor ist (0/6/0) und der Richtungsvektor ist (6/-3/0).
Das bedeutet, hier wurde der Schnittpunkt einer Geraden mit einer Ebene ermittelt, die aufeinander senkrecht stehen. Dabei geht die Gerade durch den Punkt (0/6/0).
Nachdem alles ausmultipliziert wurde, ergab sich für λ der Wert 0,8 und damit der Schnittpunkt S. Das ist das klassische Lotfußpunktverfahren, mit dem der Abstand des Punktes (0/6/0) von der verwendeten Geraden ermittelt wird.
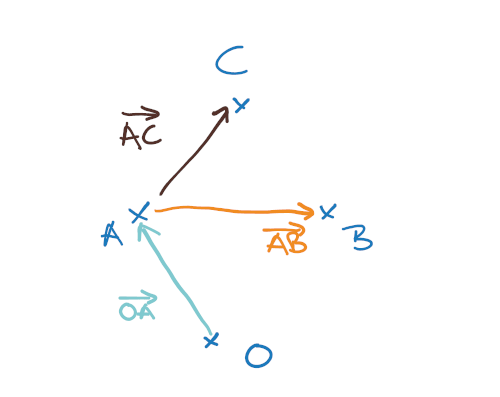
Die letzte Gleichung unten rechts beschreibt den Weg vom Ursprung 0 zum Punkt T. Dazu gehen wir von 0 zu S und dann parallel zur z-Achse senkrecht nach oben. Und zwar so weit, wie es dem Abstand vom Punkt C nach S entspricht.
Ein Blick an den Anfang der Arbeitsblattes sagt uns, dass der Punkt C die Koordinaten (3/0/0) hat. Daraus können wir die folgende Skizze zusammenstellen:
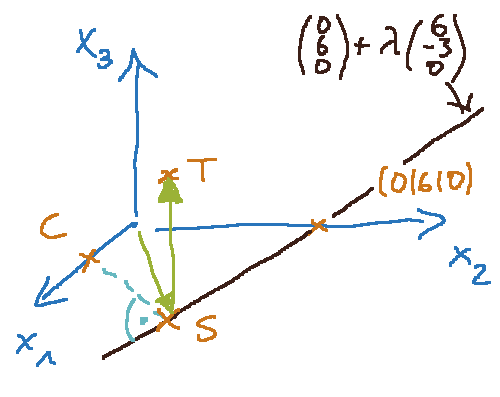
türkis: Senkrechte durch C auf diese Gerade
grün: Vektoren von 0 nach S und von S nach oben
Der Punkt T ist von der Geraden genauso weit entfernt wie der Punkt C. Die Vektoren von C nach S und von T nach S stehen senkrecht aufeinander. Also wurde der Punkt C um einen Winkel von 90° um die Gerade gedreht.
Hinter dem Term steckte also der Auftrag:
„Der mit C bezeichnete Punkt wird nach der Drehung um einen Winkel von 90° um die Gerade mit T bezeichnet. Ermitteln Sie die Koordinaten von T.“
Wichtig für diese Art von Aufgaben ist es, Muster wiederzuerkennen und Vektorgleichungen in Pfeilen als Skizze visualisieren zu können. Deshalb empfehle ich, diese Kompetenzen rechtzeitig zu trainieren.
Achsensymmetrie nachweisen
Wenn zwei Punkte bezüglich einer Achse symmetrisch sind, dann stimmen sie in der entsprechenden Koordinate überein. Die beiden anderen Koordinaten wechseln die Vorzeichen.
Beispiel Symmetrie bezüglich der x-Achse:
A(5 / 2 / 3) -> A'(5 / -2 / -3)
Eine Gerade durch A und A‘ schneidet die x-Achse senkrecht und beide Punkte sind gleich weit von der x-Achse entfernt.
In einer Aufgabe waren mehrere Punkte zum Überprüfen gegeben.
Beispiel:
B(2 / -1 / 8) und C(-2 / 1 / 8)
Diese Punkte sind symmetrisch bezüglich der z-Achse.
Körper im Koordinatensystem um eine gegebene Achse drehen
Bei dieser Aufgabenstellung liegt die Schwierigkeit darin, sich eine solche Drehung vorzustellen. Eine Skizze wurde ausdrücklich eingefordert, ansonsten müsste ich an dieser Stelle noch einmal darauf hinweisen 😉
Stelle dich darauf ein, dass du die neuen Koordinaten der Ecken eines so gedrehten Körpers ermitteln sollst.
Schnittfigur zwischen einem Körper und einer Ebene beschreiben
Auch hier ist dreidimensionale Vorstellungskraft gefragt. Wenn zum Beispiel eine Ebene durch einen Quader schneidet, kann die Schnittfigur unterschiedlich viele Ecken haben. Ein paar Beispiele:
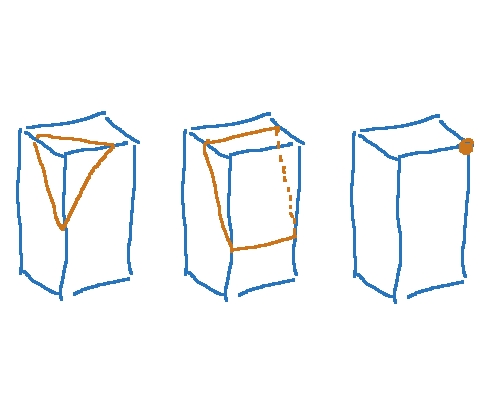
Der linke Quader wird so geschnitten, dass ein Dreieck entsteht, beim mittleren ist die Schnittfläche ein Rechteck und beim rechten liegt die Schnittebene auf der Ecke auf, sodass die Schnittmenge nur aus einem Punkt besteht.
Kooordinatenebenen und -achsen verstehen
In 65% der geometriebasierten Klausuren wurde auf die Koordinatenebenen und -achsen verwiesen. Es ist also wichtig, die dazu gehörigen Gleichungen und Richtungsvektoren im Kopf zu haben.
x-Achse
y-Achse
z-Achse
xy-Ebene
z = 0
enthaltene RV:
z-Achse entspricht dem Normalenvektor
xz-Ebene
y = 0
enthaltene RV:
y-Achse entspricht dem Normalenvektor
xy-Ebene
x = 0
enthaltene RV:
x-Achse entspricht dem Normalenvektor
Koordinate z bzw. x3 als Höhe
In den Original-IQB-Klausuren sind die Achsen mit x1, x2 und x3 beschriftet. Je nach Lehrbuch entspricht das x, y und z.
Die x3 -Koordinate wird besonders häufig als Höhe eines Objektes erfragt.
An einer Ebene spiegeln
Wird ein Punkt an einer der Koordinatenebenen gespiegelt, bleiben die entsprechenden zwei Koordinaten gleich, bei der dritten ändert sich das Vorzeichen.
Beispiel Symmetrie bezüglich der xy-Ebene:
A(5 / 2 / 3) -> A'(5 / 2 / -3)
Eine Gerade durch A und A‘ schneidet die xy-Ebene senkrecht und beide Punkte sind gleich weit von dieser Ebene entfernt.
In einer entsprechenden Aufgabe sind mehrere Punkte gegeben, die du überprüfen sollst.
Beispiel:
B(2 / -1 / 8) und C(2 / 1 / 8)
Diese Punkte sind symmetrisch bezüglich der xz-Ebene.
Manchmal soll ein Punkt an einer anderen Ebene gespiegelt werden. Dafür brauchst du den Normalenvektor dieser Ebene. Mit den Punkt als Stützvektor und dem Normalenvektor als Richtungsvektor setzt du eine Geradengleichung auf. Der gespiegelte Punkt muss auf der anderen Seite der Ebene gleich weit entfernt sein.
Mehr Details findest du weiter unten im Kapitel über Geraden und Ebenen.
Punkte im Raum
Koordinaten aus einer Abbildung entnehmen
Eine flache Abbildung auf Papier ist für die Darstellung eines Punktes mit drei Koordinaten nicht eindeutig. Trotzdem war in mehr als der Hälfte der geometriebasierten Klausuren gefordert, dass Punktkoordinaten aus einer Abbildung entnommen werden.
Dabei ging es zum Beispiel um einen Quader, bei dem von den vier unteren Ecken drei gegeben waren. Durch diese zusätzlichen Bedingungen ist dann der vierte Eckpunkt festgelegt.
Zu jedem Punkt gibt es einen Ortsvektor. Dieser Ortsvektor gibt die direkte Verbindung vom Koordinatenursprung zum Punkt an. Vektorgleichungen sind im Prinzip eine Wegbeschreibung, wie du auf indirektem Weg zum Punkt P gelangst:

In Worten bedeutet diese Gleichung, dass ich am Nullpunkt starte und über die Zwischenstationen A, B und C den Punkt P erreiche.
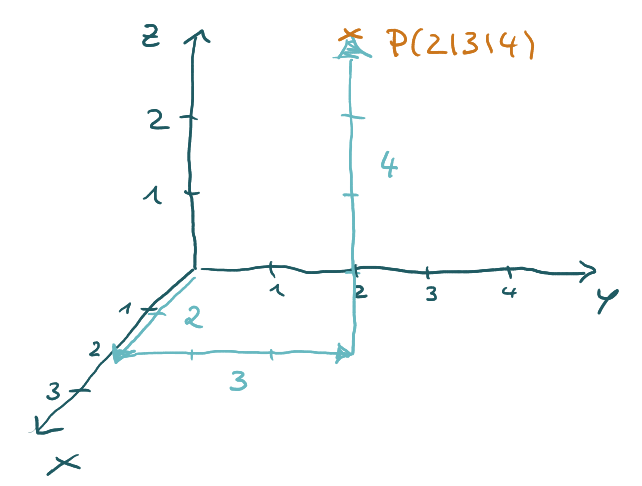
Punkte / Objekte in Abbildung einzeichnen
Hierbei ist besonders wichtig, dass du die Reihenfolge der Koordinatenachsen sicher beherrscht.
Erst nach vorne/hinten, dann nach rechts/links, dann nach oben/unten. Beachte, dass die x1-Achse kürzere Abstände zwischen den Markierungen hat.

Koordinaten eines Punktes berechnen
Zu jedem Punkt gibt es einen Ortsvektor. Dieser Ortsvektor gibt die direkte Verbindung vom Koordinatenursprung zum Punkt an. Vektorgleichungen sind im Prinzip eine Wegbeschreibung, wie du auf indirektem Weg zum Punkt P gelangst:



Wenn du keine Abbildung hast, um daraus die Koordinaten zu entnehmen, suche dir im Text die Punkte zusammen, die gegeben sind. In der Aufgabenstellung wird dir beschrieben, in welchem Verhältnis der gesuchte Punkt zu den bekannten Punkten steht.
Ist der Punkt zum Beispiel 3 Längeneinheiten über einem anderen, dann addierst du zur z-Koordinate 3.
Immer wieder ist der Mittelpunkt einer Strecke, einer Fläche oder eines Körpers gesucht. Auch hier hilft eine Skizze.
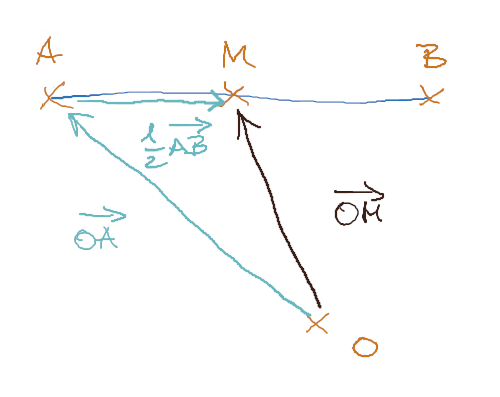

Der gesuchte Ortsvektor vom Ursprung zum Mittelpunkt M (braun) kann ersetzt werden durch die „Umleitung“ über den bekannten Ortsvektor zum Punkt A und die Hälfte des Richtungsvektors von A nach B.
Abstand zwischen zwei Punkten
Berechne dazu den Vektor zwischen den beiden Punkten (falls nicht schon gegeben). Der Betrag dieses Vektors entspricht dem Abstand. Dafür quadrierst du alle Koordinaten des Vektors, addierst sie und ziehst aus dem Ergebnis die Wurzel.
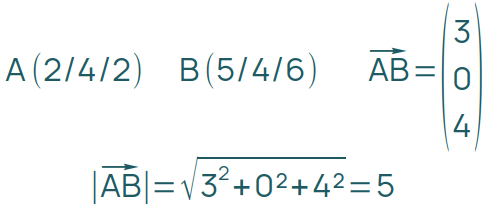
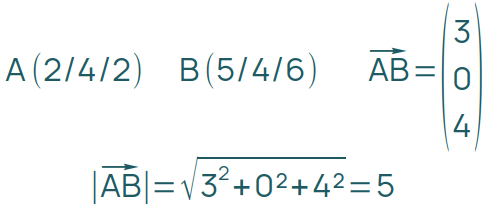
Geraden / Ebenen
Gerade aus zwei Punkten
Du kannst jeden der beiden Punkte für den Ortsvektor verwenden. Ich nehme aus Gewohnheit immer den ersten. Von diesem Punkt aus bildest du den Richtungsvektoren zum zweiten Punkt. Aus diesen Bausteinen setzt du deine Gleichung zusammen:
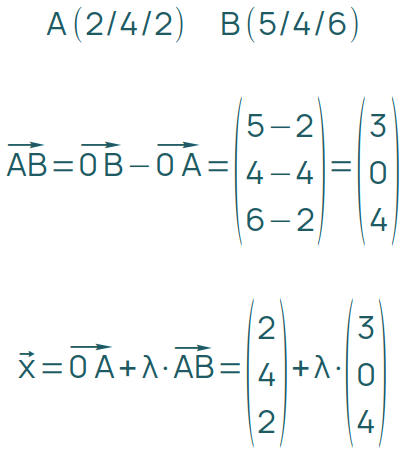
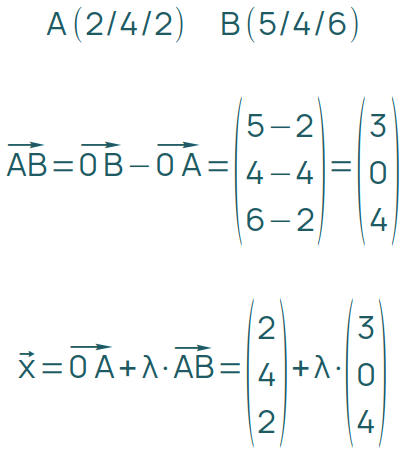
Komponenten einer Gerade verstehen
Eine vektorielle Geradengleichung in der Parameterform besteht aus einem Ortsvektor, der die Gerade im Raum befestigt, und einem Richtungsvektor, der sie im Raum ausrichtet.
Vor dem Richtungsvektor ist der sogenannte Parameter, der im Falle einer Geraden jeden beliebigen Wert annehmen kann. Am besten stellst du dir den Parameter als Schieberegler vor.


Hier kannst du dieses Prinzip auf Geogebra selbst ausprobieren.
Ebene aus drei Punkten / aus einer Gerade und einem Punkt
Das war einer der am häufigsten vorkommenden Aufgabentypen. Deswegen ist es besonders wichtig, dieses Verfahren auswendig zu können.
Meistens sind drei Punkte gegeben, in anderen Fällen musst du sie dir selbst überlegen. In allen Fällen war die Koordinatenform verlangt.
Du beginnst mit einer Ebenengleichung in Parameterform:


Du kannst jeden der drei Punkte für den Ortsvektor verwenden, ich nehme aus Gewohnheit immer den ersten. Von diesem Punkt aus bildest du die Richtungsvektoren zu den zwei anderen Punkten und setzt aus diesen drei Bausteinen diese Gleichung zusammen:



Im nächsten Schritt berechnest du aus den beiden Richtungsvektoren den Normalenvektor, der senkrecht auf deiner Ebene steht:
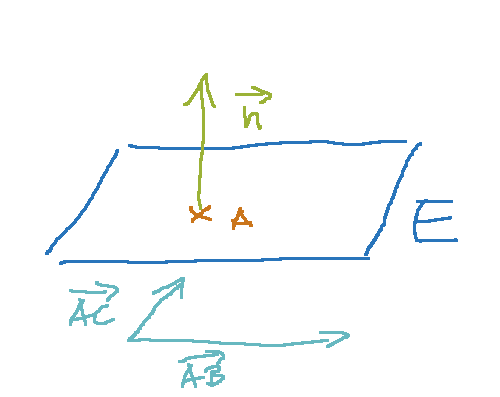

Dafür verwendest du das Kreuzprodukt. Leider steht in der Formelsammlung nur die Anleitung für das Skalarprodukt, also solltest du das Kreuzprodukt rechtzeitig trainieren.


Der Punkt A ist weiterhin der Aufpunkt für den Ortsvektor. Damit erhältst du die Normalenform:


Durch das Ausmultiplizieren der Klammer ergibt sich die Koordinatenform:
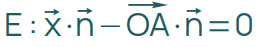
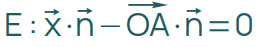
Beispiel:
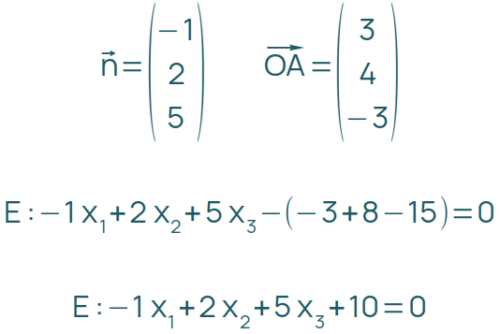
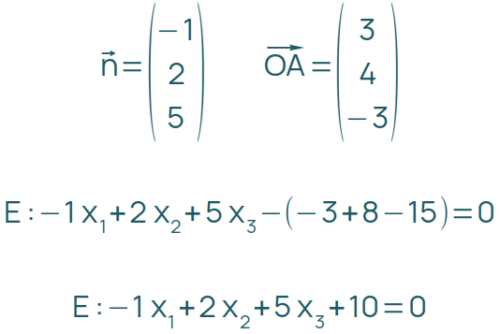
Parameterform verstehen
Die Parameterform einer Ebenengleichung sieht so aus:



Um damit möglichst frei und kreativ umgehen zu können, solltest du die Bedeutung der einzelnen Bausteine verstanden haben.
X ist ein beliebiger Punkt in der Ebene. Der rechte Teil der Gleichung ist eine Art Reisebeschreibung. Wir starten am Ursprung 0 und gehen zunächst zum Aufpunkt A.
Dann bewegen wir uns in Richtung des Vektors zwischen AB und zwar so weit, wie es der Parameter µ vorschreibt. Ist µ negativ, bewegen wir uns in die entgegengesetzte Richtung des Vektors von B nach A. Als letzten Schritt bewegen wir uns parallel zum Vektor zwischen A und C.
Die Parameter kannst du auch als Schieberegler verstehen. Hier kannst du dieses Prinzip auf Geogebra selbst ausprobieren.
Punktprobe
Oft wird gefragt, ob ein Punkt Teil einer Geraden oder einer Ebene ist. Dafür werden seine Koordinaten eingesetzt oder die Ebene/Gerade in Parameterform dem zum Punkt gehörenden Ortsvektor gleichgesetzt.
Beim Einsetzen in die Koordinatenform musst du nur ausrechnen, ob die Gleichung aufgeht.
Beim Gleichsetzen entsteht ein Gleichungssystem, das für die beteiligten Variablen gelöst werden muss. Gibt es hierbei eine Lösung, dann ist der Punkt in der Geraden oder der Ebene.
gegenseitige Lage zweier Geraden / Schnittpunkte
Zwei Geraden können sich schneiden oder identisch, echt parallel oder windschief sein. Andere Optionen gibt es im dreidimensionalen Raum nicht.
Im ersten Schritt vergleichst du die Richtungsvektoren. Ob diese parallel sind, ist auf den ersten Blick offensichtlich, wenn du den einen Vektor mit einer Zahl multiplizieren kannst und dadurch den anderen Vektor erhältst.
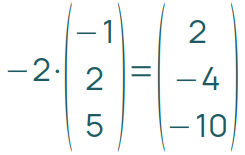
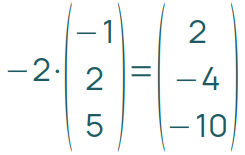
In diesem Fall machst du mit dem Ortsvektor der einen Geraden die Punktprobe mit der anderen Geradengleichung. Ist der Punkt in der anderen Geraden enthalten, sind die beiden Geraden identisch, ansonsten sind sie echt parallel.
Nicht parallele Geraden schneidest du, indem du sie gleichsetzt und das dabei entstehende Gleichungssystem löst. Hat das System keine Lösung, sind die beiden Geraden windschief.
Bei genau einer Lösung gibt es einen Schnittpunkt. Die Parameterwerte aus dieser einen Lösung setzt du in die jeweiligen Geradengleichungen ein, um den Schnittpunkt zu ermitteln.
Grundsätzlich reicht es, nur einen einen Parameter in die passende Gleichung einzusetzen. Wenn du eine Minute Zeit hast, ist es meiner Ansicht nach immer schön, auf beiden Wegen denselben Punkt zu berechnen und damit mehr Sicherheit zu haben 🙂
gegenseitige Lage zweier Ebenen / Schnittgeraden
Zwei Ebenen können sich schneiden, identisch oder echt parallel sein. Andere Optionen gibt es im dreidimensionalen Raum nicht.
Zur Bestimmung der gegenseitigen Lage eignet sich die Normalenform besonders gut: Sind die beiden Normalenvektoren parallel, dann sind es auch die beiden Ebenen.
In allen anderen Fällen ergibt sich eine Schnittgerade. In den Klausuren zwischen 2017 und 2023 war nie gefordert, dass du diese Gerade selbst berechnest, in manchen Fällen war sie allerdings gegeben und sollte kommentiert werden.
Sollte in der Zukunft mal eine Schnittgerade gefordert sein, kannst du dich mit diesem Video von MathemaTrick darauf vorbereiten 🙂
gegenseitige Lage Ebene und Gerade / Schnittpunkte
Eine Gerade kann zu einer Ebene parallel sein, diese schneiden oder in der Ebene liegen. Andere Optionen gibt es im dreidimensionalen Raum nicht.
Zur Bestimmung der gegenseitigen Lage hilft es, wenn die Ebene in der Normalenform gegeben ist: Stehen Normalenvektor der Ebene und der Richtungsvektor der Geraden senkrecht zueinander, sind die Ebene und die Gerade parallel.
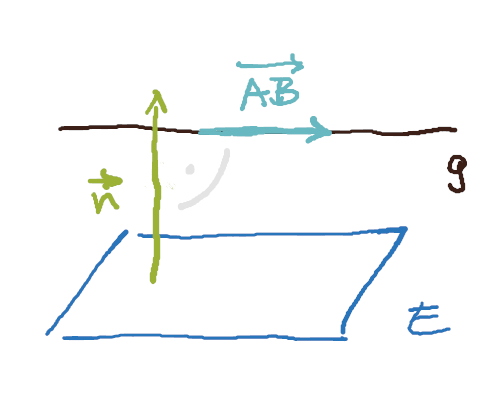

Wenn du den Aufpunkt der Geraden in die Ebenengleichung einsetzt, findest du heraus, ob er in der Ebene liegt oder nicht. Damit liegt dann auch g in E oder eben nicht.
Liegen sowohl g als auch E in der Parameterform vor, ist es auch möglich, die beiden gleichzusetzen und das entsprechende Gleichungssystem mit drei Variablen zu lösen.
Das ist im Verlgleich zum Bilden des Normalenvektors allerdings mehr Aufwand. Erstens kostet es mehr Zeit und die Optionen, sich durch einen Vorzeichenfehler zu verrechnen, sind beim Kreuzprodukt und beim Gleichungssystem ziemlich gleich.
Ist E in der Koordinatenform gegeben, liest du den Normalenvektor an der Gleichung ab:
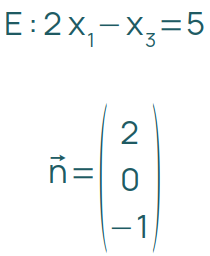
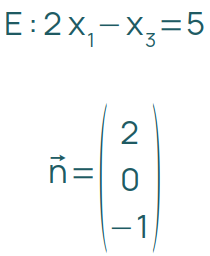
Die Koordinaten für den Normalenvektor stehen vor x1, x2 und x3 inklusive der jeweiligen Vorzeichen.
Kommt eine Koordinate in der Gleichung nicht vor, schreibst du an der Stelle im Normalenvektor eine 0.
Steht vor einer Koordinate in der Ebenengleichung keine Zahl, schreibst du in den Normalenvektor entsprechend eine 1.
Alternativ kannst du auch die vektorielle Geradengleichung in drei Gleichungen auseinander nehmen und in die Koordinatenform der Ebene einsetzen:


Wenn die letzte Gleichung eine Lösung hat, sind g und E nicht parallel. Das λ setzt du in die Geradengleichung ein und erhältst dadurch den Schnittpunkt.
Streckenverhältnisse
Regelmäßig ist das Verhältnis gefragt, in dem eine Strecke geschnitten wird. Dafür berechnest du zunächst den Schnittpunkt.
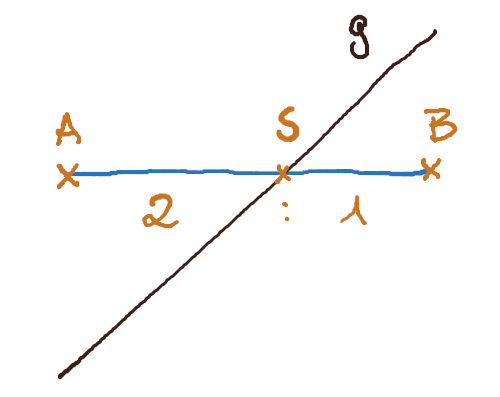

In diesem Beispiel ist S der Schnittpunkt zwischen der Geraden g und der Strecke von A nach B.
Wenn du den Abstand von A zu S und von S zu B ermittelst und den einen Wert durch den anderen teilst, hast du das Verhältnis.
Es kann vorkommen, dass S eine Variable enthält, zum Beispiel, wenn g eine Geradenschar ist. Dann enthält das Verhältnis sehr wahrscheinlich auch diese Variable.
Lotfußpunktverfahren / Abstand Punkt Ebene / Abstand Punkt Gerade
Dieses Verfahren auf dem Schirm zu haben, ist sehr hilfreich, weil es immer wieder bei Fragen nach Abständen verwendet werden muss.
Das Prinzip ist relativ übersichtlich, allerdings sind meine Schüler*innen immer wieder verwirrt, wenn sie dabei nur die Zahlen und Vektoren vor Augen haben.
Wenn wir einen Punkt und eine Ebene betrachten, dann nehmen wir den gegebenen Normalenvektor der Ebene und den Ortsvektor zum Punkt. Aus diesen beiden Komponenten setzen wir eine Gerade zusammen. Diese ist automatisch senkrecht zur Ebene (daher der Begriff Lot) und geht durch P.
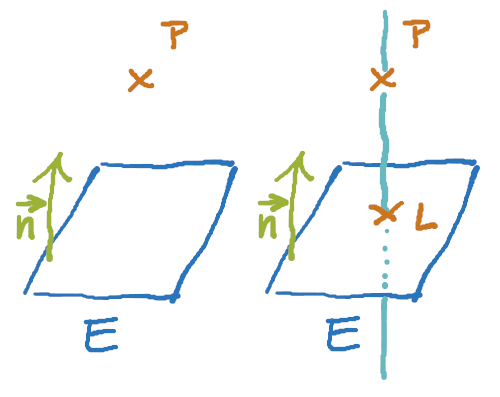

Der Schnittpunkt aus dieser Geraden und der Ebene ist der Lotfußpunkt L. Der Betrag des Vektors von P nach L ist der Abstand des Punktes von der Ebene.
Alternativ kann auch die Ebenengleichung in die Hessesche Normalen- beziehungsweise Koordinatenform umgewandelt und die Koordinaten des Punktes P eingesetzt werden. Dieses Verfahren steht allerdings leider nicht in der zugelassenen Formelsammlung.
Wenn wir einen Punkt und eine Gerade betrachten, dann nehmen wir den gegebenen Richtungssvektor der Geraden und den Orzsvektor zum Punkt. Aus diesen beiden Komponenten setzen wir eine Ebene in der Normalenform zusammen. Diese ist automatisch senkrecht zur Geraden (daher der Begriff Lot) und enthält den Punkt P.
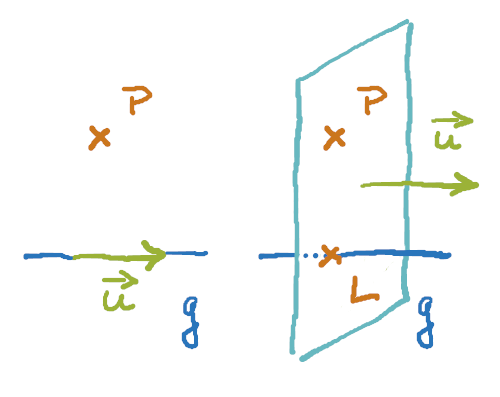
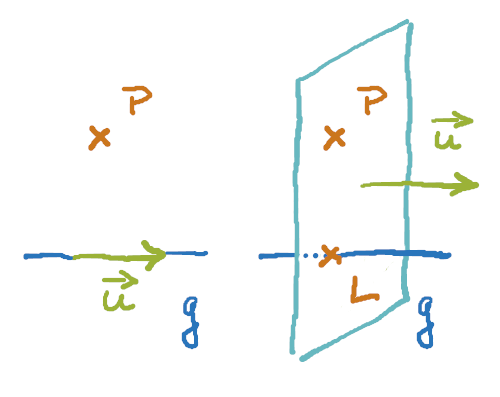
Der Schnittpunkt aus dieser Ebene und der Geraden ist der Lotfußpunkt L. Der Betrag des Vektors von P nach L ist der Abstand des Punktes von der Geraden.
In Prinzip kannst du mit diesem Verfahren auch den Abstand zweier windschiefer Geraden berechnen.
Punkt-, Geraden- bzw. Ebenenschar
Genau wie in der Analysis Funktionsscharen vorkommen, gibt es in der analytischen Geometrie Scharen von Punkten, Geraden und Ebenen. Dazu werden eine oder mehrere Zahlen in den Koordinaten der beteiligten Vektoren durch Variablen ersetzt.
Eine Beispielfrage könnte lauten:
„Für welches k enthält die Ebene E den Punkt P?“
In solchen Fällen behandelst du die Variable zunächst wie eine Zahl und rechnest je nach Situation mutig los. In der Beispielfrage ging es darum, ob der Punkt in der Ebene liegt. Dafür machst du einfach eine Punktprobe, setzt als den Punkt mit der Ebene (in Parameterform) gleich oder setzt ihn (in die Koordinaten- oder Normalenform) ein.
Ganz am Ende deiner Rechnung steht dann die Variable der Lösung gegenüber.
Mein Tipp ist wirklich immer, erst einmal mit dem anzufangen, was du hast und was du kannst. Wenn du die Rechenverfahren verstanden hast und sicher beherrschst, kannst du auch mit Scharen umgehen 🙂
Flächen / Körper
Spezielle geometrische Figuren nachweisen
Der erste Schritt sollte immer sein: Mach dir eine Skizze!
Folgende Figuren kamen teils mehrfach vor:
Ein gleichschenkliges Dreieck hat zwei gleich lange Seiten. Entsprechend musst du zwei Vektoren mit gleichen Beträgen finden.
Für ein rechtwinkliges Dreieck musst du zwei Vektoren finden, die zueinander senkrecht stehen.
Für ein Rechteck musst du zwischen den beteiligten Vektoren mit dem Skalarprodukt rechte Winkel nachweisen. Dass die gegenüberliegenden Vektoren identisch sind, siehst du ihnen an, sobald du sie berechnet hast,
Beim Quadrat ist über das Rechteck hinaus noch zu berechnen, dass alle vier Seiten gleich lang sind.
Beim Parallelogramm ist nachzuweisen, dass die gegenüberliegenden Seiten identische Vektoren liefern.
Beim Trapez müssen zwei gegenüberliegende Seiten parallel, aber nicht gleich lang sein. Die Längen und Richtungen der anderen beiden Seiten sind irrelevant.
Flächeninhalte berechnen
Die relevanten Formeln für Dreiecke, Parallelogramme, Trapeze, Kreise und Drachenvierecke stehen in der Formelsammlung. Du musst nur die Formeln für Rechtecke und Quadrate auswendig wissen 🙂
In den meisten Aufgaben ist die eigentliche Schwierigkeit, dass du die Koordinaten der beteiligten Eckpunkte finden und Abstände berechnen musst.
Beim Dreieck und beim Parallelogramm ist es auch möglich, statt der aus der Mittelstufe bekannten Formeln das Vektorprodukt zu verwenden. Dieser Zusammenhang sollte dir geläufig sein:
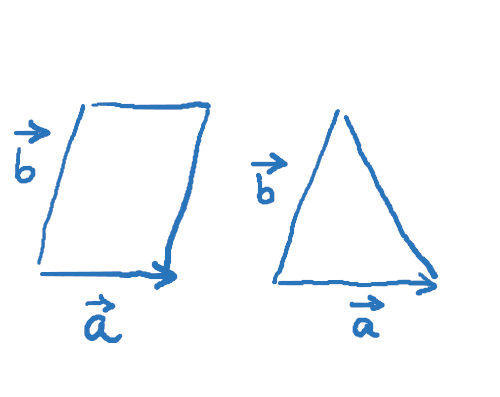
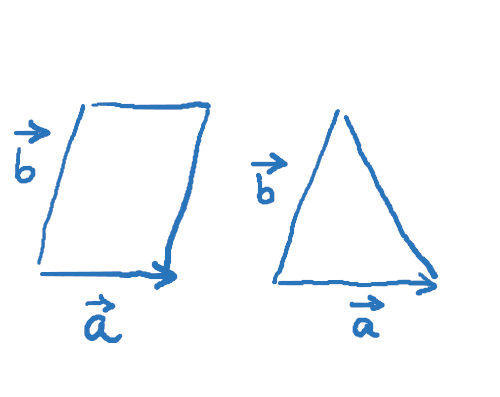
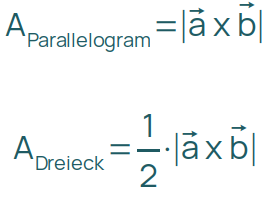
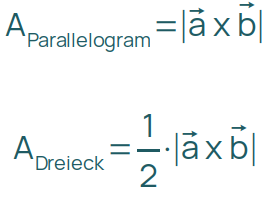
Du berechnest also das Vektorprodukt (auch Kreuzprodukt genannt) und im Anschluss den Betrag des Ergebnisvektors.
Pyramidenvolumen berechnen
Die Formeln für das Volumen der Spitzkörper Pyramide und Kegel stehen in der Formelsammlung. Dafür musst du die relevanten Eckpunkte und Abstände ermitteln.
Alternativ ist es auch möglich, das Volumen einer Pyramide mit dreieckiger Grundfläche durch das Spatprodukt zu berechnen. Dieser Zusammenhang sollte dir geläufig sein.


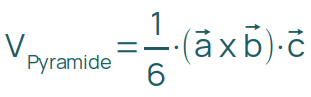
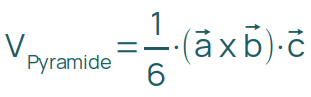
Volumen eines Prismas berechnen
Die Formel für Prismen steht in der Formelsammlung. Sie gilt auch für Quader, falls du vor lauter Stress auf dem Schlauch stehst 🙂
Volumen eines zusammengesetzen Körpers berechnen
Immer wieder kommen Körper vor, die komplizierter aussehen. Deine Aufgabe ist es, sie in Quader, Prismen und Pyramiden zu zerlegen, die Einzelvolumina zu berechnen und am Ende zusammen zu addieren.
Eine Pyramide mit einer viereckigen Grundfläche schneidest du in zwei Pyramiden mit jeweils dreieckiger Grundfläche. Die beiden kleineren Teile berechnest jeweils du mit dem Spatprodukt.
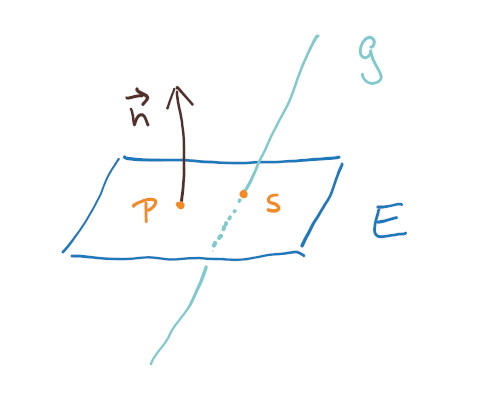

Winkel
Bedeutung des Skalarproduktes
Das Skalarprodukt zeigt dir, ob zwei Vektoren senkrecht zueinander stehen, wenn es Null ist.
An dieser Stelle: Die Begriffe „senkrecht“, „orthogonal“ und „rechtwinklig“ bedeuten alle genau dasselbe, und zwar einen Winkel von 90° 😀
Ist das Skalarprodukt nicht Null, kannst du den Winkel zwischen den beiden Vektoren ermitteln. Die Formel dazu (und auch, wie du das Skalarprodukt berechnest) steht in der Formelsammlung.
Du brauchst das Skalarprodukt und die Beträge der beiden beteiligten Vektoren. Den cos-1 berechnet dein Taschenrechner.
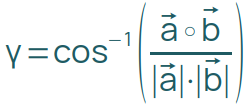
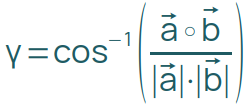
Neigungswinkel
Oft wurde nach dem „Neigungswinkel einer Ebene zur Horizontalen“ gefragt. Das bedeutet:
In welchem Winkel steht die Ebene zur xy-Ebene, also zur „Bodenplatte“ des Koordinatensystems?
Dafür musst du den Winkel zwischen dem z-Vektor und dem Normalenvektor der betrachteten Ebene berechnen.


Schnittwinkel zwischen Ebenen und/oder Geraden
Der Schnittwinkel zwischen zwei Geraden ist der Winkel zwischen ihren zwei Richtungsvektoren.
Der Schnittwinkel zwischen einer Gerade und einer Ebene ist 90° abzüglich dem Winkel zwischen dem Richtungswinkel der Geraden und dem Normalenvektor der Ebene.
Der Schnittwinkel zwischen zwei Ebenen ist der Winkel zwischen ihren zwei Normalenvektoren.
Gerade senkrecht / parallel zu einer Ebene
Sollst du eine Gerade durch einen gegebenen Punkt und senkrecht zu einer Ebene aufstellen, ist der Punkt der Aufpunkt und der Normalenvektor der Ebene der Richtungsvektor der Geraden.
Wenn du eine beliebige Gerade durch einen Punkt und parallel zu einer Ebene nennen sollst, ist der Punkt wieder der Aufpunkt. Für den Richtungsvektor bildest du einen Vektor senkrecht zum Normalenvektor der Ebene. (Siehe nächster Punkt „Senkrechte zu einer Geraden“)
Senkrechte zu einer Geraden
Sollst du ganz allgemein eine Senkrechte zu einer Geraden g angeben, verwendest du ihren Aufpunkt für den Ortsvektor der neuen Geraden. Für den Richtungsvektor wandelst du den Richtungsvektor von g folgendermaßen um:
Setze eine Koordinate auf Null, vertausche die anderen beiden Koordinaten und ändere bei einer der beiden Zahlen das Vorzeichen.
Beispiel:
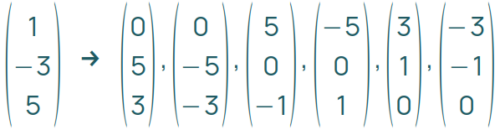
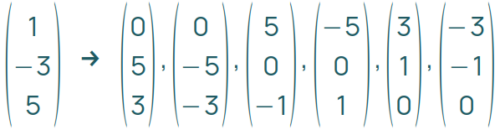
Bewegungen
Längeneinheiten umrechnen
Du solltest auf dem Schirm haben, wie du km, m, dm, cm und mm ineinander umrechnest.
Es kam mehrfach vor, dass einer Längeneinheit oder [LE] im Sachzusammenhang eine bestimmte Länge zugeordnet wurde und das bei der Antwort auf eine Frage mitbedacht werden musste.
Unter anderem entsprach einmal 1 [LE] der Länge von 80cm. Fehlte die abschließende Umrechnung in der Antwort, kostete das Punkte.
Bedeutung des Richtungsvektors für Bewegungen oder Lichtstrahlen
Der Richtungsvektor einer Geraden kann entlang einer Kante eines Körpers verlaufen. Er ist aber besonders interessant in Aufgaben, in denen er in die Richtung zeigt, in die sich etwas bewegt, oder in die ein Lichtstrahl leuchtet.
Regelmäßig wird in einer Abiturklausur Vektorrechnung verglichen, in welcher Beziehung eine Bewegung zu den Himmelsrichtungen steht. Oder zur sogenannten Horizontalen, die mathematisch gesehen die xy-Ebene ist, auf der der z-Vektor (0/0/1) senkrecht steht.
Vektoren sind Größen, die eine Richtung und einen Betrag, oder anders gesagt eine Länge haben. Diese Länge wird in Sachaufgaben oft verwendet, um die Geschwindigkeit einer Bewegung anzuzeigen.
Du hast vermutlich während deiner Zeit in der Oberstufe Aufgaben gerechnet, in denen Flugzeuge durch die Gegend fliegen. Genau diese Art Sachaufgaben bieten sich für Abituraufgaben an. Daher ist es sinnvoll, wenn du dich vorher darauf einstellst und dir das Konzept dahinter noch einmal verdeutlichst.
Schnittpunkt mit Ebenen außerhalb oder innerhalb einer Fläche
Immer wieder ist zu beurteilen, ob ein Gegenstand eine gegebene Fläche berührt. Das kann eine Wand oder Mauer, aber auch ein eingegrenztes Stück auf dem Boden sein.
Um das herauszufinden, schneidest du die Gerade, auf der sich der Körper bewegt, mit der Ebene, in der die Fläche liegt. Dann musst du vergleichen, ob der Schnittpunkt von den Koordinaten her zwischen den Eckpunkten der begrenzten Fläche liegt oder nicht. (Am besten mit Hilfe einer Skizze!)


Es gab auch zwei Klausuren, in deren Geschichten sich ein Ball auf einer Parabelbahn bewegte. Dafür war eine Schar von Punkten gegeben, in der der Parameter t für die Zeit in Sekunden stand.
P(32 − 8t / 5 / −5t 2 + 6,5t + 0,3)
Wenn gefragt ist, wo der Ball den Boden berührt, setzt du die z-Koordinate gleich null und löst die Gleichung nach t auf. Nur eine positive Zeit ist im Sachzusammenhang sinnvoll, weil der Ball ja nicht in die Vergangenheit fliegt. Und dieses t setzt du noch bei der x-Koordinate ein:
−5t 2 + 6,5t + 0,3 = 0 -> t1 = 1,34 und t2 = -0,04
32 – 8 · 1,34 =21,28 -> P(21,28 / 5 / 0)
Diese Koordinaten gleichst du dann wie oben beschrieben mit den Eckpunkten der Fläche ab.
Wenn gefragt ist, ob der Ball in einer Fläche auf einer beliebigen Ebene auftrifft, setzt du P in diese Ebene ein, erhältst t und damit wieder die Koordinaten des Schnittpunktes.
Schattenkonstruktion
In mehr als einer Klausuraufgabe war ein Schatten zu konstruieren. Auch wenn das nach Physik klingt und vielleicht irgendwie schwierig, ist es nur wieder das Schneiden von Geraden (Lichtstrahlen) mit Ebenen (Wände, Erdboden).
Wenn es um Sonnenlicht geht, ist der Richtungsvektor immer gegeben. Du nimmst einen Eckpunkt des beleuchteten Körpers für den Ortsvektor und fertig ist die Geradengleichung. Sobald dir klar ist, auf welche Ebene der Schatten fällt, kannst du den Schnittpunkt und damit einen Eckpunkt des Schattens berechnen.
Wenn es um eine Lampe (sogenannte „punktförmige Lichtquelle“) geht, sind ihre Koordinaten gegeben. Diesen Punkt nimmst du für den Ortsvektor. Aus dem Ort der Lampe und dem Eckpunkt des Körpers berechnest du den Richtungsvektor der Geraden. Schon hast du die Geradengleichung für deinen Lichtstrahl, den du dann mit der Wand schneiden kannst.
Wie immer: Mach dir am besten eine Skizze 😉
Zeiteinheiten
Du solltest auf dem Schirm haben, wie du Stunden, Minuten und Sekunden ineinander umrechnest. Vor allem, wenn es um Geschwindigkeiten geht.
Es könnte sein, dass sich aus einer Abbildung eine Strecke in Metern und eine Zeit in Sekunden ergibt, du aber die Geschwindigkeit in Kilometer pro Stunde angeben sollst.
1 km/h ≈ 0,278 m/s
1 m/s = 3,6 km/h
Geschwindigkeit ermitteln
Grundsätzlich brauchst du dafür die Strecke, um die sich ein Körper bewegt hat, und die Zeit, die er dafür brauchte. Dann teilst du die Strecke durch die Zeit.
Wenn der Richtungsvektor die Geschwindigkeit repräsentiert, musst du seinen Betrag ermitteln.
Beispiel:
In der folgenden Geraden g haben die Koordinaten die Einheit Meter, der Parameter λ hat die Einheit Sekunde.
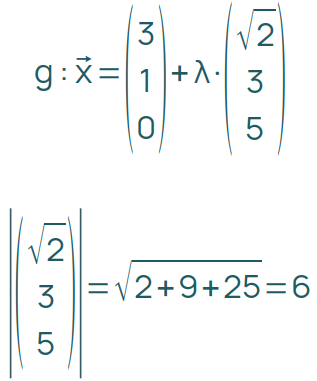
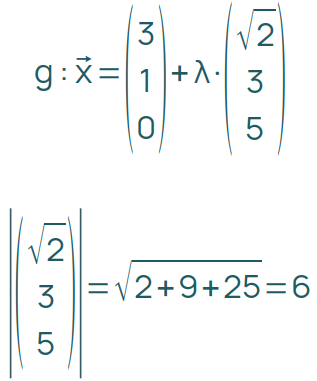
Die Geschwindigkeit ist in diesem Fall 6 m/s.
Themenbereich Matrizen
Die Aufgaben mit Matrizen kamen in ungefähr 30% der IQB-Klausuren vor. Ein großer Teil meiner Schüler*innen hat im Mathematikunterricht über Matrizen nichts gehört. Ein paar von ihnen holen dieses Thema gerade noch nach, allerdings nicht in dem Umfang, dass sie dem Anspruch der IQB-Klausuren gewachsen wären.
Die zentralen Abiturprüfungen sind klar geregelt (PDF-Dokument): Die Lehrkräfte an den jeweiligen Schulen in Schleswig-Holstein wählen aus den zwei zentralen Vorschlägen eine Abiturklausur Vektorrechnung aus, die die Prüflinge bearbeiten müssen.
Ich gehe davon aus, dass dabei in den meisten Fällen die Matrizenklausuren heraus genommen werden. Trotzdem werde ich in diesem Artikel diesen Aufgabentyp besprechen, auch weil er in Zukunft wichtiger werden könnte.
Die Hintergrundgeschichten waren Austauschprozesse. Das können Tierpopulationen sein, Verhältnisse von Stimmen bei einer Wahl, aber auch Leuchtmuster in LED-Installationen. Es gab nur eine kurze Nebenaufgabe mit einer Matrix ohne Sachzusammenhang.
Theoretisch könnten auch zukünftig Aufgaben mit Matrizen gestellt werden, die Körper oder Flächen unter anderem stauchen, drehen oder spiegeln. Dieser Aufgabentyp kam allerdings in den Jahren 2017 bis 2023 gar nicht vor.
Diese Konzepte wurden immer wieder abgefragt:
- Interpretation einer Matrix und ihrer Elemente im Sachzusammenhang
- Rechenverfahren mit Matrizen
- Übergangsdiagramme erstellen oder auswerten
- zukünftige, vergangene und stabile Populationen berechnen
- inverse Matrizen und ihre Bedeutung
Übergangsdiagramme
Übergangsdiagramm auswerten
Oft fangen Matrizenaufgaben mit einem Übergangsdiagramm an. Zum Beispiel wechseln Wähler*innen von einer Partei zu einer anderen und zurück. Oder Insekten legen Eier, aus denen Larven werden und letztendlich wieder neue Insekten.
Du solltest in der Lage sein, die Zahlen an den Pfeilen in deinen eigenen Worten erläutern zu können. Beispielsweise so:
„Innerhalb eines Jahres wechseln 80% der Kundinnen der Marke A zur Marke B, während 35% der Kundinnen der Marke B zur Marke A übergehen.“
Es ist immer wieder die Aufgabe, nachzuvollziehen, wie aus einem solchen Übergangsdiagramm eine Übergangsmatrix entstanden ist und einzelne noch fehlende Elemente in der Matrix nachzutragen.
Übergangsdiagramm erstellen
In ein paar Klausuren bestand eine Aufgabe darin, aus einem ausformulierten Text ein Übergangsdiagramm zu zeichnen.
Dieses Diagramm muss keinen Schönheitspreis gewinnen. Es reicht, wenn die Pfeile deutlich erkennbar in die richtige Richtung zeigen und die Zahlen korrekt angebracht sind.
Es ist für die spätere Rechnung zu empfehlen, Prozentzahlen gleich in Dezimalzahlen umzuwandeln. Also statt 85% schreibst du 0,85, statt 2% schreibst du 0,02. Dann brauchst du im Anschluss nur noch zu multiplizieren, statt dir einen Dreisatz zu überlegen.
Beispiel: 35% von 250 €
Als Dreisatz:
| € | % |
|---|---|
| 250 | 100 |
| 2,50 | 1 |
| 87,50 | 35 |
Als Multiplikation:
250 € · 0,35 = 87,50 €
Die Matrix im Sachzusammenhang
einzelne Elemente erläutern, Zahlen zuordnen
Dir sollte geläufig sein, dass in einer Übergangsmatrix die Elemente angeben, wie viel % von einem Zustand in einen anderen wechseln.
Beispiel:


Im Sachzusammenhang wandern zum Beispiel 60 % der Kundinnen von A nach C, während 70% der Kundinnen von B ihrer Marke treu bleiben.
Bei Produktionsmatrizen ist die Richtung von -> nach umgekehrt:
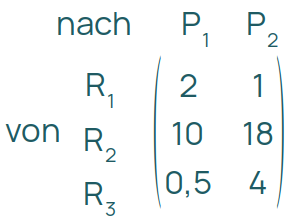
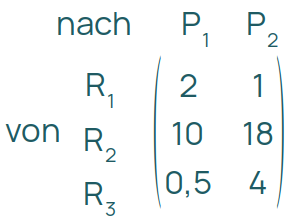
In diesem Beispiel werden für das Produkt P1 10 Einheiten des Rohstoffes R2 gebraucht, während für das Produkt P2 4 Einheiten des Rohstoffes R3 nötig sind.
räumliche Interpretation eines Verteilungsvektors
In einem Fall sollte ein Vektor, der die Verteilung verschiedener Menschen auf drei Gruppen beschrieb, als Ortsvektor im dreidimensionalen Raum betrachtet und in ein Koordinatenzentrum eingezeichnet werden.
Wenn wir davon ausgehen, dass die Gesamtzahl dieser Menschen sich nicht ändert, ist damit die Länge des Vektorpfeiles begrenzt. In der Aufgabe sollte das entsprechend argumentiert werden. Es war die Frage, ob der zum Verteilungsvektor gehörende Punkt außerhalb eines gegebenen Quaders liegen könnte.
richtige Auswahl für verschiedene Aufgabenstellungen
In Aufgaben zu Produktionsprozessen werden mehrere Matrizen angegeben: Von den Rohstoffen zu den Zwischenprodukten und von den Zwischenprodukten zu den Endprodukten. Manchmal ergeben sich zwischenzeitlich auch Matrizen von den Rohstoffen direkt zu Endprodukten. In manchen Fällen waren letztere von Anfang an gegeben.
Zur Beantwortung verschiedener Fragen ist es wichtig, dass du aufpasst und jeweils die richtige Matrix auswählst. Manchmal haben die Matrizen die gleichen Anzahlen an Zeilen und Spalten. Dann hilft ein Blick in das Diagramm und ein Vergleich der Zahlen „von -> nach“.
Rechnen mit Matrizen
Multiplikation mit einem Skalar
Ein Skalar ist eine Zahl ohne Richtung im Gegensatz zu einem Vektor.
Wird eine Matrix mit einem Skalar multipliziert, dann wird jedes Element der Matrix mit dem Skalar multipliziert.
In einer Matrixklausuraufgabe war der Betrag eines solchen Skalars gefragt. Im Prinzip musst du für die Antwort zwei Matrizen vergleichen und überlegen, um welchen Faktor sie sich unterscheiden.
Beispiel:


Die beiden Matrizen unterscheiden sich in allen Elementen um den Faktor 3. Das ist also der gesuchte Skalar.
Multiplikation zweier Matrizen / einer Matrix mit einem Vektor
Die Matrizenmultiplikation ist vom rein rechnerischen Verfahren her einfach, der wichtigste Punkt ist, dass du dich konzentrierst und darauf achtest, dass du immer eine Zeile mit einer Spalte verbindest.
Dieses Video von MathemaTrick zeigt dir das Verfahren in Aktion.
Übergangsmatrizen zu einer übergeordneten Matrix kombinieren
In Produktionsprozessen gibt es Matrizen von Rohstoffen zu Zwischenprodukten (RZ) und von den Zwischenprodukten zu den Endprodukten (ZE). Eine immer weder gefragte übergeordnete Übergangsmatrix drückt den Prozess von den Rohstoffen zu den Endprodukten aus (RE).
Du erhältst RE durch Multiplikation:
RE = RZ · ZE
In Aufgaben mit Tier- oder Pflanzenpopulationen ist es möglich, zum Beispiel von einem Jahr zum nächsten zu rechnen. Hier sollst du regelmäßig Matrizen für größere Zeiträume angeben oder das Verfahren beschreiben, wie solche Matrizen berechnet werden können.
Du erhältst die Matrix für größere Zeiträume durch Potenzieren. Gilt die Matrix A zum Beispiel für ein Jahr und du sollst einen Term für eine Zehn-Jahres-Matrix B angeben, sieht die Antwort so aus:
B = A10
Es ist realistisch, dass du den Term so stehen lassen sollst, ohne ihn auszurechnen. Denn so eine lange Reihe von Multiplikationen hintereinander bringt nichts außer Zeitaufwand und ist ein schöner Anlass, sich zu verrechnen.
Ist eine Matrix C für einen Rhythmus von zwei Jahren gesucht, wird nicht nur eine Beschreibung des Vorgehens erwartet. In diesem Fall berechnest du tatsächlich:
C =A · A
Zufügen/Streichen von Spalten/Zeilen
Es gab Aufgaben zu Produktionsabläufen, in denen eine Firma ein neues Endprodukt E4 einführte. Im Ergebnis wurde die Rohstoff-Endprodukt-Matrix um eine Spalte erweitert.
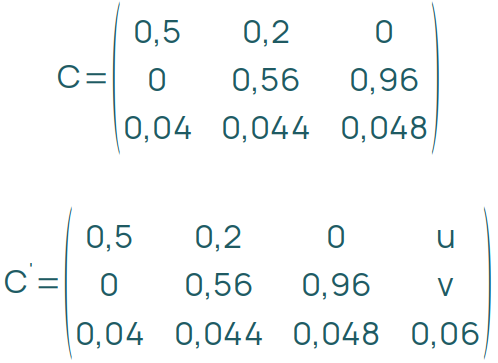
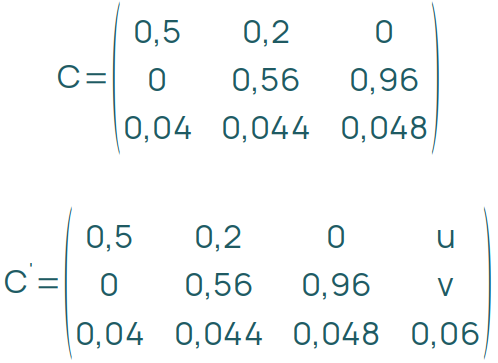
Die Fragestellung lautete:
„Ermitteln Sie die Summe der Mengeneinheiten der Zwischenprodukte, die zur Herstellung einer Mengeneinheit von E4 erforderlich ist.“
An dieser Stelle begann der Lösungsweg damit, auf der ersten Seite des Arbeitsblattes die Matrizen zu finden, die den Übergang von den Rohprodukten zu den Zwischenprodukten und von den Zwischenprodukten zu den Endprodukten E1 bis E3 beschreiben:


An der Herstellung der Zwischenprodukte ändert sich nichts, A kann also unverändert weiterverwendet werden.
B lässt sich um die unbekannten Mengen der Zwischenprodukte Z1 und Z1 erweitern, die für E1 gebraucht werden:


Jetzt muss dir klar sein, dass C‘ = A · B‘ ist. Wenn du A mit B‘ multiplizierst und das Ergebnis mit C‘ vergleichst, siehst du, dass
0,04 · x + 0,04 · y = 0,06 -> x + y =1,5
Die Summe aus x und y ist auch schon direkt die Antwort auf die Frage. Was hier zur Lösung der Aufgabe notwendig ist, ist ein Verständnis des Konzeptes hinter der Berechnung von Prozessen.
Solltet ihr also Matrizen behandelt haben, kann es also sein dass eine entsprechende Klausur verwendet wird und du nicht nur geübte Verfahren abarbeiten musst. Solltest du an einer Stelle im Text das Gefühl haben, dass dir Informationen fehlen, lies noch einmal den Anfang des Arbeitsblattes.
In anderen Aufgaben wurde von einem Monat zum nächsten ein Restaurant geschlossen. Die Personen in der Geschichte hatten daher keine Möglichkeit mehr, zu diesem Restaurant zu wechseln. Einen Monat lang galt deswegen eine andere Matrix:


Die drei Zeilen und drei Spalten gelten jeweils für die drei Restaurants. Aus der dritten Zeile ist ablesbar, dass in diesem Monat niemand mehr nach R3 wechselt. Aus der dritten Spalte ist ablesbar, dass von R3 40% der Personen zu R1 wechseln und 60% zu R2.
Eine Frage lautete:
„Begründen Sie, dass aus der Verteilung im Monat nach der Schließung mithilfe des Modells nicht auf die Verteilung der Kunden unmittelbar vor der Schließung geschlossen werden kann.“
Wenn du N zum „Rückwärtsrechnen“ einsetzt, bekommst du ein Gleichungssystem ohne eindeutige Lösung. Für Fragen des Musters „Begründen Sie, dass nicht“ rate ich dazu, das Gegenteil der Behauptung anzunehmen, also hier dass es möglich ist, zurück zu rechnen. Auf dieser Basis machst du so lange weiter, bis du auf einen Widerspruch stößt. Dieser Widerspruch ist deine Begründung.
Generell wird immer wieder danach gefragt, welche Matrix sich von welcher herleiten lässt und welche nicht. Wenn zum Beispiel die Kund*innen eines Stromtarifs nochmal in zwei unterschiedliche Gruppen aufgeteilt werden, lassen sich die beiden neuen Anteile zum alten Wert zusammenaddieren.
10 % der Personen in Tarif A1, 15% in Tarif A2 -> 25% der Personen in der übergeordneten Kategorie A
30 % der Personen in Kategorie B -> Wie sich diese Personen in B1 und B2 aufteilen, ist nicht vorhersehbar.
Populationen berechnen
in die Zukunft
Um eine Population im nächsten Zeitabschnitt (je nach Aufgabe Jahr, Monat oder Tag) zu berechnen, multiplizierst du die Übergangsmatrix mit dem aktuellen Populationsvektor.
Etwas komplizierter wird es, wenn du mehrere Zeitabschnitte in die Zukunft rechnen sollst.
In einer Aufgabe war eine Matrix gegeben für eine Wolfspopulation bezogen auf einen Ein-Jahresrhythmus. Betrachtet wurden weibliche Tiere im Alter von einem, zwei und mindestens drei Jahren. 72% der Tiere sollten in den ersten zwei Lebensjahren sterben, gefragt war nach dem Wert für x:


Die übergeordnete Matrix im Zweijahresrhytmus enthält dem Term 0,7x an der Stelle, die angibt, welcher Anteil der einjährigen Tiere eines Jahrgangs nach zwei Jahren noch leben und dann in die Gruppe der mindestens drei Jahre alten Tiere übergehen. Wenn 72% von ihnen sterben, sind noch 28% übrig:
0,7 x = 0,28 -> x = 0,4
Im Sachzusammenhang bedeutet das, dass von den einjährigen Wölfinnen 40% das Alter von zwei Jahren erleben. In dieser Altersklasse ist, anders herum gesagt, die Sterblichkeit 60%.
Manchmal ist der aktuelle Populationsvektor nicht gegeben, aber eine bestimmte zukünftige Verteilung gefordert, zum Beispiel, dass drei beteiligte Gruppen gleich groß sind, also alle einen Anteil von 1/3 haben. Dann nimmst du einen aktuellen Vektor (x/y/z) an, multiplizierst die Matrix damit und setzt das Produkt dem geforderten Vektor gleich. Dieses Verfahren läuft rechnerisch genauso wie das Rechnen in die Vergangenheit, siehe nächster Punkt.
in die Vergangenheit
Um eine Population im vorherigen Zeitabschnitt (je nach Aufgabe Jahr, Monat oder Tag) zu berechnen, multiplizierst du die Übergangsmatrix mit einem unbekannten Populationsvektor (x/y/z) und setzt dieses Produkt dem aktuellen und bekannten Populationsvektor gleich:
Das kann folgendermaßen aussehen:
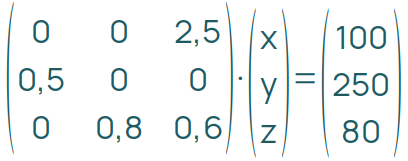
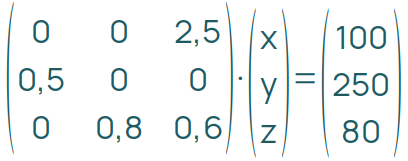
Durch Ausmultiplizieren erhältst du ein Gleichungssystem:


Als Lösung erhältst du x = 500, y = 70 und z = 40. Das sind die Bestandszahlen vom letzten Jahr, Monat oder Tag, je nach Aufgabe.
Die Variablen x, y, und z können natürlich, je nach Geschichte anders heißen. Zum Beispiel e für Eier, l für Larven und s für Schmetterlinge 🦋
stabile Populationen
Eine übliche Aufgabe fragt nach einer „stabilen Verteilung“ oder einer Population „die sich nicht mehr verändert“. Der dazu gehörende Vektor wird auch als Fixvektor bezeichnet, weil der Zustand der Population ab diesem Zeitpunkt fixiert ist.
Dafür multiplizierst du die Matrix mit einem unbekannten Vektor und setzt das Produkt dem unbekannten Vektor gleich. Mit anderen Worten suchst du also nach dem Vektor, der bei diesem Vorgehen selbst wieder herauskommt. Du kannst die Matrix beliebig oft wieder mit diesem Vektor multiplizieren, das Ergebnis ist immer wieder dasselbe.
Das könnte beispielsweise so aussehen:


Durch Ausmultiplizieren erhältst du ein Gleichungssystem:
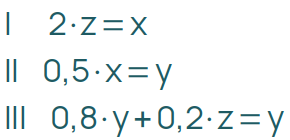
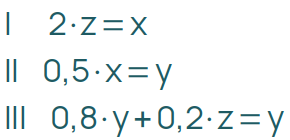
Dieses Gleichungssystem hat keine eindeutige Lösung, weil nach dem „Aufräumen“, also dem Verschieben aller Variablen auf die linke Seite, rechts vom Gleichheitszeichen in jeder Gleichung eine Null steht.
Um ein Ergebnis zu erhalten, musst du für eine der Variablen eine konkrete Zahl vorgeben (die in der Aufgabe genannt wird). Soll zum Beispiel x= 100 sein, ergibt sich der Vektor (100/50/50).
Alternativ sollst du davon ausgehen, dass alle Tiere/Pflanzen zusammengezählt 100% entsprechen, also x + y + z = 1 ergibt. Damit bekommst du im vorliegenden Fall einen eindeutigen Vektor von (0,5/0,25 /0,25). Eine unendliche Anzahl möglicher stabiler Verteilungen sind Vielfache dieses Vektors.
Sollte das Gleichungssystem tatsächlich keine Lösung haben, gibt es keinen Fixvektor.
größte / kleinste mögliche Veränderungsrate ermitteln
In einer Klausur wurde das Wechselverhalten zwischen drei Stromtarifen betrachtet mit folgender Übergangsmatrix:
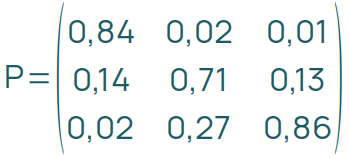
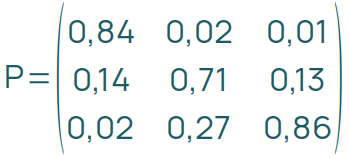
Eine Frage lautete:
„Für den Anteil aller Kunden, die von einem Monat zum nächsten den Tarif wechseln, gibt es im Modell einen kleinsten und einen größten möglichen Wert. Geben Sie diese beiden Werte an und begründen Sie Ihre Angabe.“
Wenn du die Frage genau liest, geht es darum, im welchen Fällen die meisten Menschen bei ihrem Tarif bleiben und in welchen die wenigsten. Dafür ist die Diagonale von links oben nach rechts unten zuständig: x · 0,84 + y · 0,71 + z · 0,86 ist der prozentuale Anteil der Personen, die nicht wechseln.
Die Extreme im Wechselverhalten ergeben sich das Setzen von Nullen und Einsen im Verteilungsvektor. Wenn alle Personen im dritten Tarif sind, werden 86% dabei bleiben und 14% in die beiden anderen Tarife wechseln. Eine geringere Anzahl von Wechseln ist nicht erreichbar.
Wenn alle Personen im ersten Tarif sind, bleiben 84% dabei und 16% wechseln.
Wenn alle Personen im zweiten Tarif sind, bleiben nur 71% in ihrer Kategorie und 29% wechseln in die anderen Tarife.
Die Antwort lautet also: Der größte Wert ist 0,29, der kleinste ist 0,14.
Eignung eines Modells im Vergleich mit der Realität
Die Beurteilung eines Modells hat nur begrenzt mit Mathematik zu tun. Meist geht es darum, dass wir davon ausgehen können, dass die Umweltbedingungen einer Tierpopulation nicht unendlich lange exakt gleich bleiben. Deswegen beschreibt die Übergangsmatrix die Veränderungen nur für einen endlichen Zeitraum.
Bezogen auf Marktprozesse kann eine Übergangsmatrix nur eine begrenzte Zahl von Jahren sinnvoll angewendet werden, bevor ein neues Produkt oder sogar eine technologische Weiterentwicklung auf den Markt kommt, ein neues Restaurant eröffnet wird oder ein Wirtschaftssystem sich durch politische Vorgänge stark verändert.
inverse Matrizen
Verfahren zum Invertieren
In den Klausuren 2017 bis 2023 war keine Berechnung einer inversen Matrix gefordert.
Dieses Video von MathemaTrick beschreibt das grundsätzliche Verfahren, falls du es trotzdem zur Sicherheit noch einmal wiederholen willst.
Interpretation im Sachzusammenhang
Im Zusammenhang mit Austausch- oder Produktionsprozessen bedeutet die inverse Matrix den „Übergang in die Vergangenheit“ oder das Schließen von Rohstoffmengen auf die Mengen der Endprodukte.
Nur quadratische Matrizen können eine inverse Matrix haben. Nicht jede quadratische Matrix ist invertierbar.
Ist eine Matrix quadratisch, aber nicht nicht invertierbar, ist kein Rückschluss auf frühere Populationen möglich. Dieser Zusammenhang war unter anderem in Matrizenklausuren gefragt.
Einheitsmatrix
Eine Einheitsmatrix enthält nur Nullen und Einsen. Die Version mit drei Zeilen und drei Spalten sieht so aus:
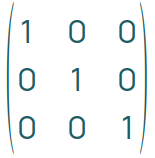

Einheitsmatrizen sind immer quadratisch und können unterschiedlich groß sein.
Sie kommen heraus, wenn du eine quadratische Matrix mit ihrer inversen Matrix multiplizierst. In einer der Klausuren zu Matrizen war genau dieser Zusammenhang gefragt. Es sollte also erkannt werden, dass eine der beteiligten Matrizen die inverse zur anderen war.
Wie gehe ich entspannt in die Abiturklausur Vektorrechnung?
Jetzt hast du einen Überblick, was dich in der Abiturklausur Vektorrechnung erwartet. Eine gute fachliche Vorbereitung ist schon die halbe Miete, auch für eine möglichst große innere Entspannung. Was kannst du zusätzlich während und in der Zeit vor der Prüfung tun?
Einer meiner am häufigsten wiederholten Tipps ist: „Mach dir eine Skizze!“ Weil ich davon so überzeugt bin, habe ich dazu einen eigenen Blogartikel geschrieben. Das Gehirn entspannt, wenn wir zunächst die Informationen aus einer Aufgabe grob auf Papier visualisieren.
Viele Dinge, die im Text unverständlich klingen, werden mit Hilfe einer bildlichen Darstellung oft viel offensichtlicher. Das betrifft ganz besonders geometrische Aufgabenstellungen.
Zusätzlich kannst du eine für dich passende Entspannungstechnik lernen. Dazu gibt es online Anleitungen für Meditationen, Atemtechniken, Affirmationen und ähnliche Methoden. Ich selbst habe eine geführte Meditation zur Stärkung der inneren Sicherheit vor Prüfungen geschrieben.
Fragen und Feedback
Diese Artikelreihe liegt mir besonders am Herzen. Und zwar, weil ich aus nächster Nähe sehe, wo die Schwierigkeiten liegen: Darin, die Aufgabenformulierungen überhaupt erst einmal zu verstehen und im generellen Druck, den die ungewisse Prüfungssituation erzeugt. Ich möchte deswegen dazu beitragen, dass möglichst viele Menschen vor ihrer Abiturklausur hilfreiche Informationen erhalten.
Wenn du Fragen zur Abiturklausur Vektorrechnung hast oder zu meinem Artikel etwas anmerken möchtest, freue ich mich sehr über Rückmeldung. Gerne auch aus anderen Bundesländern 🙂
Und wenn du jemanden in deinem Umfeld hast, der oder die 2024 Matheabi schreiben wird, freue ich mich, wenn du diesen Artikel mit dieser Person teilst.
Alle Blogartikel zur Mathematik findest du hier.






Schreibe einen Kommentar