Warum sind auch in der Oberstufe Skizzen für Textaufgaben so sinnvoll und entlastend? Ich erkläre es dir und zeige dir an ein paar Beispielen, wie einfach du sie anfertigen kannst.
Textaufgaben (auch Sachaufgaben genannt), sind allgemein nicht bei allen Menschen beliebt. Bei meinen Schüler:innen in der Oberstufe ist das nicht anders. Je komplexer die Geschichte scheint, umso ausführlicher rollen die Augen. Skizzen können oft sehr helfen, Dinge zu vereinfachen, so dass du sie leichter verstehst.
In der Mittelstufe sind Skizzen oft noch Pflicht. Zum Beispiel in Arbeiten über den Pythagoras oder bei der Konstruktion von Dreiecken.
Später werden sie nicht mehr eingefordert. Der Schwerpunkt liegt zunehmend auf eigenverantwortlichem Arbeiten. Und auf sich alleine gestellt, lassen viele diese scheinbar unnötige Vorarbeit ausfallen. Dabei ist es mit steigender Komplexität der Aufgaben umso wichtiger, dass wir den Überblick behalten.
Was bringen mir Skizzen für Textaufgaben in der Oberstufe?
Wenn es einen Satz gibt, den ich in meinem Unterricht am häufigsten wiederhole, ist es dieser:
„Mach dir eine Skizze! Die muss nicht schön sein und auch nicht maßstäblich, aber mach dir eine Skizze!“
Warum rate ich zu Skizzen für Textaufgaben? Da gibt es mehrere Gründe:
- Während du eine Skizze anfertigst, beschäftigst du dich intensiv mit dem Text der Sachaufgabe.
- Erstmal etwas zu zeichnen, lenkt vom gefühlten Druck ab, etwas in kurzer Zeit korrekt rechnen zu müssen.
- Du entlastest dein Gehirn, wenn du Informationen zu Papier bringst, statt zu versuchen, sie alle nebeneinander nur in deiner Vorstellung aufzureihen.
- Du kannst in dieser Zeichnung während der Bearbeitung der Aufgabe neu dazukommende Informationen nachtragen (besonders bei Kurvendiskussionen) und die Plausibilität von Lösungen schnell erkennen.
- Es gibt immer wiederkehrende Aufgabentypen, nur in unterschiedliche Geschichten verkleidet. Eine einfache und systematische Skizze hilft dir, einen Aufgabentyp, den du schon einmal erfolgreich bearbeitet hast, zu erkennen.
- Unterm Strich spart eine Skizze Zeit, die du ansonsten mit Grübeln verbringen würdest.
Was ist eine Skizze und was ist sie nicht?
Eine Skizze besteht aus möglichst einfachen Grundelementen und wird mit Variablennamen und Zahleninformationen beschriftet. Mit etwas Übung zeichnest du sie in unter einer Minute.
Damit du sie eventuell anpassen kannst, ist es sinnvoll, eine Skizze mit Bleistift anzufertigen. Ideal ist eine Größe von 10 cm · 10 cm, damit das Ganze nicht zu klein wird. Wichtige Elemente kannst du mit Buntstiften hervorheben.
Was du für eine Skizze nicht brauchst, ist ein Lineal. Du musst auch deine Skizze nicht nach dem gleichen Schema zeichnen wie jemand anders, sondern so, dass du sie verstehst.
Meistens ist eine Skizze nicht explizit gefordert. Dann bekommst du auch keine Bewertung dafür. Sie dient nur als grafischer Notizzettel für dich. Du kannst im Verlauf der Bearbeitung der Aufgabe noch immer weiter daran werkeln und sie verfeinern.
Was sind Grundelemente bei Skizzen für Textaufgaben?
Ich habe einen Verdacht: Oft vermeiden (meine) Schüler:innen Skizzen, weil sie glauben, das sei irgendwie kompliziert. Ich sage es gerne immer wieder: Die Skizze muss nicht schön aussehen und auch nicht maßstäblich korrekt sein.
Ich bin sicher, du kannst Kreise, Vierecke, Dreiecke, Strichfiguren, Linien und Pfeile zeichnen. Mehr brauchst du im Grunde nicht, auch nicht bei Textaufgaben in der Oberstufe.
Schöner und ordentlicher als in dieser Abbildung muss es nicht sein.
Wie gehe ich beim Skizzieren vor?
Ich persönlich lese erst einmal den Text ganz durch. Dann nehme ich meinen Bleistift und lese die Aufgabe noch einmal schrittweise. Ich stelle mir die beschriebene Geschichte möglichst plastisch vor. Jedes Element der Geschichte, das in mir ein Bild erzeugt, zeichne ich. Zum Beispiel eine Person, eine Kiste, einen Apfel.
Wenn zwischen zwei Elementen der Geschichte eine Beziehung besteht, zeichne ich sie in die Skizze ein. Für ein Flugzeug, das von A nach B fliegt, mache ich einen Pfeil. Wenn in einer Kiste zehn Birnen sind, zeichne ich ein Viereck mit zehn Kringeln darin. Bei guter Laune sind die Kringel birnenförmig.
Wenn sich während der weiteren Bearbeitung Zahlen oder neue Beziehungen ergeben, füge ich sie der Skizze zu.
Beispiel Analysis
Oft geht es bei einer Komplexaufgabe in Analysis um einen zeitlichen Verlauf. Stell dir vor, eine Person bekommt per Tropf ein Medikament verabreicht und du sollst die Konzentration im Blut betrachten.
In so einem Fall zeichne ich ein einfaches Koordinatensystem und eine kurvige Linie. Wie gesagt, nicht maßstäblich, nur als Aufhänger für Rechenansätze und als grafischen Notizzettel.
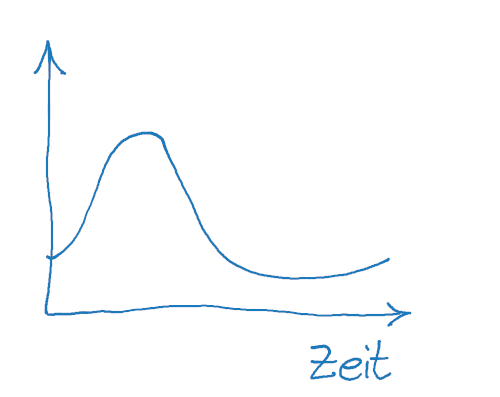
Bei der weiteren Bearbeitung der Aufgabe füge ich dann eventuelle Hochpunkte, Wendepunkte, Tangenten oder ähnliches zu.
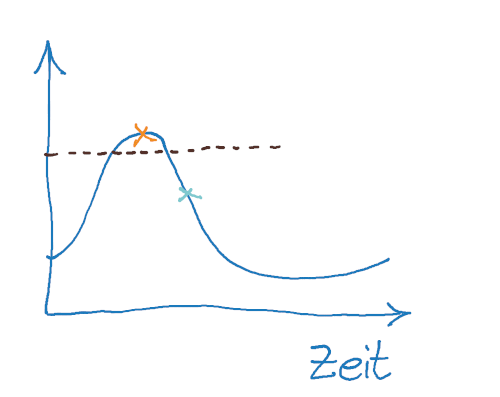
Manchmal ist gefragt, in welchem Zeitraum ein bestimmter Wert überschritten wird. Dafür kann ich eine Horizontale in meine Skizze einfügen. Dadurch sehe ich leichter, wie ich Anfang und Ende der Zeitspanne ausrechnen kann. Nämlich als Schnittpunkte der Geraden mit der Originalfunktion.
Beispiele Stochastik
Manchmal sollen Menschen auf Plätzen verteilt sitzen. Dann deute ich die Stühle als Halbkreise an. Hier zum Beispiel sollen Anton und Bert auf den äußeren Plätzen sitzen. Drei weitere Kinder verteilen sich auf die übrigen Stühle:
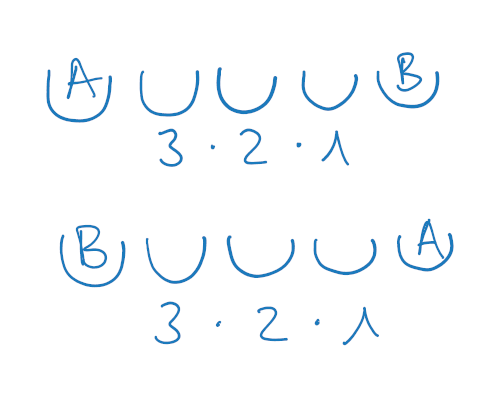
Das ist jetzt ein relativ einfaches Problem. Am Bild sehen wir aber, dass es zwei Möglichkeiten gibt, Anton und Bert zu platzieren. Für den zweiten Platz von links stehen drei Kinder zur Verfügung, für den mittleren noch zwei und für den vierten Platz nur noch eins.
Diese Zahlen kann ich direkt darunter schreiben und miteinander multiplizieren. Das Schema funktioniert auch, wenn die Geschichten komplizierter werden.
Bei einem Hypothesentest kann ich die an einem Konflikt Beteiligten wie in einem mittelmäßig spannenden Comic zeichnen.
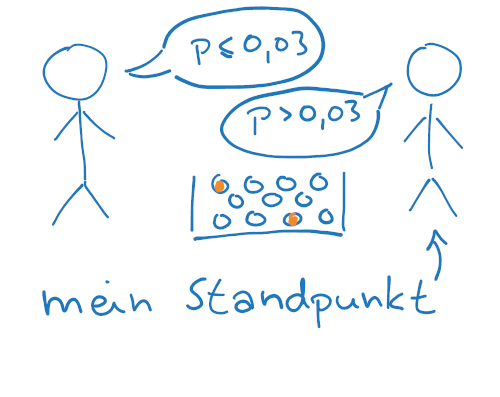
Um welches Produkt es geht, ist hierbei austauschbar. Wichtig ist, dass du in der Skizze die Person identifizierst, deren Perspektive du vertreten sollst. Und schon weißt du, welches die Nullhypothese und welches die Gegenhypothese (bzw. Alternativhypohese) ist.
Du stehst auf der Seite der Gegenhypothese. Die entsprechende Figur kannst du dann noch einmal farbig nachziehen.
Bei einer hypergeometrischen Verteilung kannst du eine Schüssel als Halbkreis zeichnen. Dort hinein zeichnest du die Dinge, die du ziehen sollst, als unterschiedlich gefärbte Kreise. Darunter listest du auf, wie viele Kreise insgesamt in der Schüssel sind und wie viele jeweils von welcher Farbe. Außerdem, wie viele insgesamt gezogen werden und wie viele jeweils von welcher Farbe.
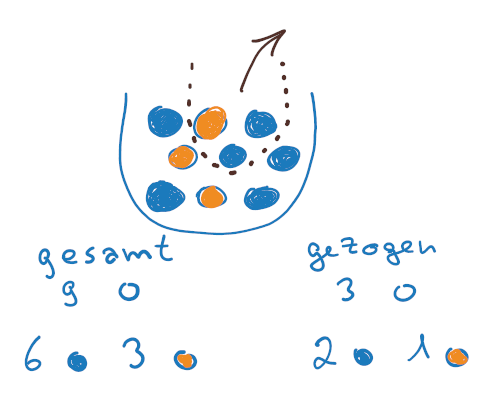
Und damit hast du genau die sechs Zahlen visualisiert, die du für die Formel der hypergeometrischen Verteilung brauchst.
Beispiele Vektorrechnung
Oft beginnen Vektoraufgaben mit drei Punkten. Die hast du in ein paar Sekunden auf das Blatt gezaubert:
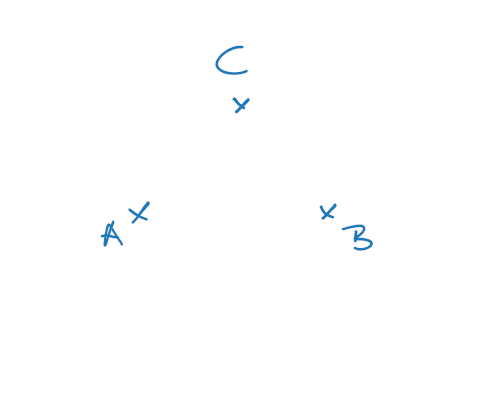
Ich füge noch einen Nullpunkt und ein paar Pfeile zu. Das dauert noch einmal ein paar Sekunden. Und schon habe ich alle Bauteile für eine Ebene beisammen:
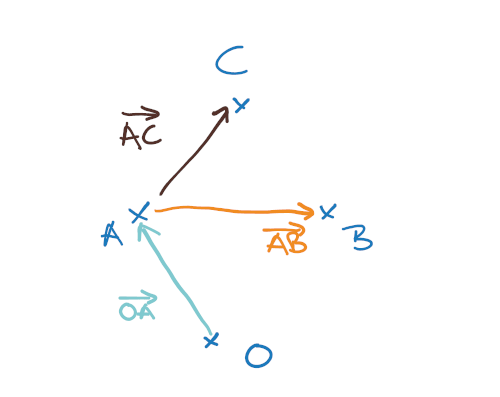
So scheinbar unspektakulär und so hilfreich. Vor allem hilft die Wiederholung bei jeder neuen Aufgabe, dass sich das Prinzip einer Ebenengleichung einprägt. Und dass dir auffällt, wie oft du eigentlich denselben Zusammenhang rechnest. Nur die dahinter stehende Geschichte variiert.
Für ein letztes Beispiel schneide ich eine Ebene und eine Gerade:
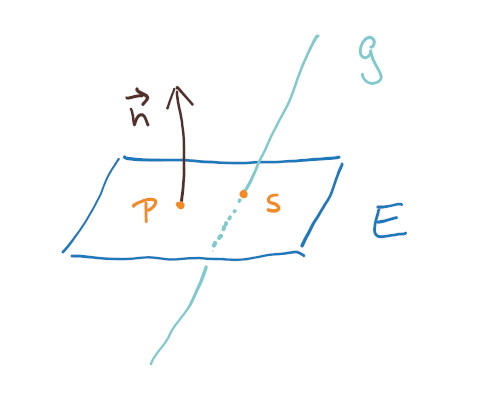
Und wieder habe ich das Bild in wenigen Sekunden fertig. Es kann sein, dass sich nachher heraus stellt, dass die Gerade die Ebene nicht schneidet. Oder darauf senkrecht steht. Für die Skizze ist das egal, sie soll nur den Rechenansatz anschaulicher machen.
Hast du noch Fragen?
Dies ist der erste Beitrag zum Thema Oberstufenmathematik. Mein Plan ist es, genau die Stellen zu klären, an denen es oft knirscht. Die weiteren Beiträge werden sich um wiederkehrende Formulierungen drehen.
Wie sieht es bei dir aus, machst du in Mathe Skizzen? Hilft dir das? Hast du die Schulzeit schon lange hinter dir? Kennst du Menschen, die heute noch mit Textaufgaben hadern?
Wenn du Fragen, Anregungen oder Anmerkungen hast, würde ich mich sehr freuen, von dir zu hören.
Falls du dich gerade auf das Matheabi vorbereitest: Dieser Blogartikel fasst alle meine Beiträge zum Thema zusammen:



Schreibe einen Kommentar