Was gehört dazu? Welche Aufgaben kommen oft dran?
Der HMF-Teil im Mathe-Abi ist nicht halb so mysteriös, wie er scheint. Ich habe die IQB-Aufgaben für dich gesichtet und erzähle dir, was oft vorkam und wie du die Aufgaben angehst.
Meine Nachhilfeschüler:innen sind aktuell auf der Zielgeraden zur Abiturklausur in Mathematik. Und vielleicht betrifft dich das ja auch. Nachdem ich über die Komplexaufgaben in Analysis, Stochastik und Vektorrechnung gebloggt habe, ist heute der hilfsmittelfreie Teil dran.
Dieser Artikel ist zu deiner Information gedacht, aber auch als Abhakliste, was du schon sicher kannst. Und zur Planung, was du noch unbedingt wiederholen solltest. Ich habe Details und Tipps angefügt, die du durch Klick auf den jeweiligen Stichpunkt sichtbar machen kannst. Im Laufe der Zeit werde ich eventuelle neue Informationen noch ergänzen.
In Schleswig-Holstein werden die Abiturklausuren 2024 auf den IQB-Poolaufgaben basieren. Daher fokussiere ich mich mit dieser Artikelserie auf diese öffentlich einsehbaren Übungsaufgaben. Und zwar zunächst auf die Dokumente zum erhöhten Niveau aus den Jahren 2017 bis 2023.
Ich plane auch Blogposts zum grundlegenden Niveau. Allerdings wird dies wenigstens in Schleswig-Holstein für das Mathe-Abi 2024 noch dezentral geregelt. (Prüfungsregelungen als PDF)
Wichtig: Natürlich kann der HMF-Teil im Mathe-Abi zukünftig Aufgaben enthalten, die von meiner Liste nicht abgedeckt sind.
Dieser Blogartikel fasst alle meine Beiträge zur Vorbereitung auf das Matheabi zusammen:
Warum sind Klausuren vergangener Jahre interessant?
Viele Abituraufgaben im Fach Mathe wiederholen sich über die Jahre immer wieder. Das gilt besonders im hilfsmittelfreien Teil. Er enthält oft Klassikerfragen, die abklopfen, wie gut du die grundlegenden Konzepte verstanden hast.
Wenn du die häufig vorkommenden Inhalte im Blick hast und diese bei deiner Vorbereitung gut übst, hat das zwei Vorteile:
- Du kannst diese Aufgaben schneller und zuverlässiger erledigen und hast dann mehr Zeit für die kniffeligeren Fragen. Manche Fragen im hilfsmittelfreien Teil lassen sich grundsätzlich in unter einer Minute beantworten.
- Du bist von vornherein entspannter. Das steigert deine Erfolgsaussichten ähnlich nachhaltig wie ein solides Faktenwissen.
Was bedeutet „HMF-Teil“?
Dieser Teil wird auch als taschenrechnerfrei bezeichnet. Wie schon im Vorabi bekommst du einen Stapel kurzer Aufgaben, die du ohne Formelsammlung und ohne Taschenrechner lösen musst.
In Schleswig-Holstein bekommt deine Schule für diesen Teil der Abiturprüfung zehn Aufgaben zugeschickt. Sie fallen in eine einfachere und eine schwierigere Kategorie.
Vier Aufgaben gehören zur Aufgabengruppe 1. Zwei dieser Aufgaben sind aus dem Bereich Analysis, jeweils eine aus der Vektorrechnung und der Stochastik.
Sechs Aufgaben gehören zur Aufgabengruppe 2. Dabei beziehen sich jeweils zwei Aufgaben auf die Analysis, die Vektorrechnung und die Stochastik.
Die Aufgabengruppe 1 musst du komplett bearbeiten, bei der Aufgabengruppe 2 darfst du zwei Aufgaben frei auswählen. Insgesamt hast du inklusive Einlesen und Auswählen 100 Minuten Zeit.
Die Zeit ist so bemessen, dass du pro Aufgabe zehn Minuten zur Verfügung hast. Die reine Berechnungszeit ist allerdings bei manchen Aufgabentypen eher unter einer Minute. Die größte Hürde ist es eher, den richtigen Ansatz zu finden.
Allgemeine Tipps
Die Zahlen sind meist glatt im Kopf berechenbar. Die Aufgaben sind in sich abgeschlossene kleine Pakete. Das hat den Vorteil, dass am Verständnis einer Aufgabe nicht noch eine darauf aufbauende Anschlussfrage hängt.
Ein genereller Tipp: Wenn du als Ergebnis einen Term wie zum Beispiel 2·ln(3) oder 8·π heraus bekommst, ist das kein Zeichen, dass du dich verrechnet hast. Solche Terme sollst du an der Stelle so stehen lassen. Es geht nicht darum, dass am Ende immer eine „schöne“ Zahl steht.
Du solltest grundsätzlich Terme vereinfachen und Gleichungen umstellen können.
Rechengesetze
Ohne Formelsammlung lernst du diese grundsätzlichen Gesetze am besten gründlich auswendig:
Ausklammern
Dieser Teil der Termumformung ist in diversen Aufgabentypen wichtig, gleichzeitig für viele Menschen zunächst etwas mysteriös. MathemaTrick hat zu diesem Thema zwei Erklärvideos: Video eins und Video zwei.
Potenzgesetze
Du solltest mindestens folgende Regeln auswendig wissen:
a^m\cdot a^n=a^{m\cdot n}\\\quad\\\frac{1}{a}=a^{-1}\\\quad\\ \sqrt{a}=a^{0,5}=a^{\frac{1}{2}}\\\quad\\a^0=1Die letzte Regel brauchst du besonders häufig.
pq-Formel
Oft ergeben sich quadratische Gleichungen, wenn zum Beispiel in der Stochastik p mit (1-p) multipliziert wird, wenn in der Analysis Nullstellen gesucht sind oder der Parameter für eine vektorielle Ebenenschar ermittel werden soll.
An dieser Stelle brauchst du ohne Taschenrechner die pq-Formel. Wenn ein schlimmer Ohrwurm aus deiner Sicht ein zumutbarer Preis dafür ist, diese Formel auswendig zu können, hier gibt es den pq-Formel-Rap.
x_{1,2}=-\frac{p}{2}\pm\sqrt{\bigg(\frac{p}{2}\bigg)^2-q}Körper
Quader
Ein Quader hat sechs rechteckige Seitenflächen. Das Volumen berechnest du aus den Kantenlängen a, b und c so:
V_{Quader}=a\cdot b\cdot cSpat
Auch ein Spat hat sechs Seitenflächen. Davon sind jeweils zwei parallel zueinander liegende Parallelogramme.
Das Volumen berechnest du aus den Kanten a, b und c mit Hilfe des Spatpoduktes. Das ist aber eher ein Fall für den Komplexaufgabenteil.
Pyramide
Eine Pyramide hat eine Grundfläche und eine Spitze. Das Volumen berechnest du im hilfmittelfreien Teil aus dem Flächeninhalt der Grundseite G und der Höhe h so:
V_{Pyramide}=\frac{1}{3}\cdot G\cdot hZylinder
Dagegen hat ein Zylinder eine kreisförmige Grundfläche G und eine Höhe h. Daraus ergibt sich das Volumen so:
V_{Zylinder}=G\cdot hFiguren
Quadrat
Ein Quadrat hat vier gleich lange Seiten und vier rechte Winkel. Den Flächeninhalt berechnest du so:
A_{Quadrat}=a\cdot aRechteck
Das Rechteck hat jeweils zwei gegenüber liegende gleich lange Seiten und vier rechte Winkel. Den Flächeninhalt berechnest du so:
A_{Rechteck}=a\cdot bParallelogramm
Ein Parallelogramm hat jeweils zwei gegenüber liegende gleich lange und parallele Seiten. Den Flächeninhalt berechnest du aus der einen Seite und der Höhe h so:
A_{Parallelogramm}=a\cdot hTrapez
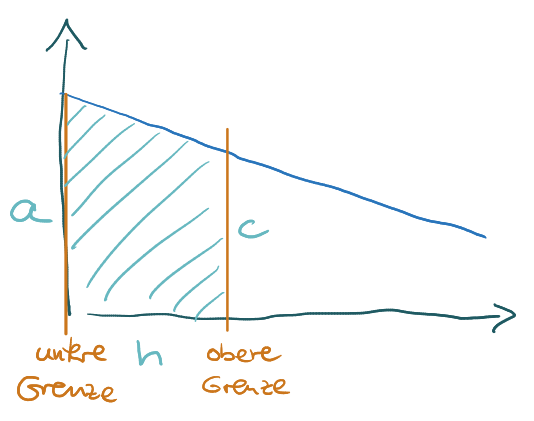
Auch ein Trapez hat zwei gegenüber liegende parallele Seiten a und c. Den Flächeninhalt berechnest du aus den beiden Seiten und der Höhe h so:
A_{Trapez}=\frac{a+c}{2}\cdot hTrapeze kommen im Analysisteil öfter mal vor, wenn es um Flächeninhalte unter den Graphen linearer Funktionen geht. Dafür musst du vielleicht das Blatt um 90° drehen.
Raute
Eine Raute hat vier gleich lange Seiten. Die jeweils gegenüber liegenden Seiten sind parallel.
Gleichseitiges Dreieck
Ein gleichseitiges Dreieck hat drei gleich lange Seiten, wie der Name schon sagt. Die drei Winkel sind auch gleich und betragen jeweils 60°.
Gleichschenkliges Dreieck
Beim gleichschenkligen Dreieck sind nur zwei Seiten und damit auch zwei Winkel gleich.
Rechtwinkliges Dreieck
Ein rechtwinkliges Dreieck hat einen rechten Winkel. Die beiden kurzen Seiten sind die Katheten, die lange Seite heißt Hypothenuse. Den Flächeninhalt berechnest du aus den Katheten a und b so:
A_{rechtw.Dreieck}=\frac{1}{2}\cdot a\cdot bIn den folgenden Listen sind die Aufgabentypen nach Häufigkeit sortiert. Je weiter oben ein Thema steht, umso häufiger wurde es abgefragt.
Analysis
Es kamen rationale Funktionen, Sinus- und Kosinusfunktionen, e‑Funktionen und in seltenen Fällen auch gebrochen rationale Funktionen vor. Es lohnt sich also, das Aussehen und generelle Verhalten dieser Funktionstypen zu wiederholen.
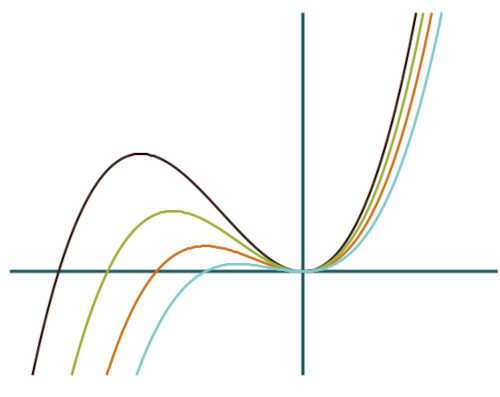
Kurvenscharen
Wichtig ist, dass du den Scharparameter beim Integrieren und Ableiten wie eine konstante Zahl behandelst. Es wird nicht nach a abgeleitet!
Beispiel:
f_a(x)=ax^2-5x\\\quad\\\implies f^{\prime}_{a}(x)=2ax-5und
F_a(x)=\frac{a}{3}x^3-\frac{5}{2}x^2+CHäufig soll aus einer Bedingung der Scharparameter bestimmt werden. Dafür bildest du zunächst das Integral, den Hochpunkt oder was auch immer gefragt ist, sodass der Parameter noch im Ausdruck drin steht. Diesen Term setzt du dann mit der Bedingung gleich, zum Beispiel mit einer bestimmten Fläche. Am Ende löst du nach dem Parameter auf.
Es gibt Aufträge der folgenden Sorte:
Zeigen Sie, dass das Flächenstück, das die Graphen von fk und fk +1 in den Grenzen von 0 bis 4 einschließen, für alle Werte von k den gleichen Inhalt hat.
Dafür berechnest du das Integral über fk in den gegebenen Grenzen. Dann setzt du in diesen Term (k+1) statt k ein. Die beiden Terme setzt du gleich. Wenn die beiden Flächen für alle k gleich sein sollen, muss das k beim Versuch, danach aufzulösen, aus der Gleichung herausfallen.
Geradengleichungen / Konzept Steigung
Immer wieder sollen Geradengleichungen angegeben werden. Unter anderem geht es dabei um Tangenten oder rechtwinklig schneidende Geraden.
Diese allgemeine Gleichung solltest du kennen:
y=m\cdot x+n
(Es kann sein, dass das n bei dir im Unterricht auch b war.)
Dabei ist m die Steigung. Bei einer Tangente ist m gleich der ersten Ableitung an dieser Stelle, also f'(x).
Bei einer senkrecht schneidenden Geraden ist
m=-\frac{1}{f^{\prime}(x)}Der Achsenabschnitt n ist häufig gefragt. Dafür setzt du die drei bekannten Werte für x, y und m ein und löst nach n auf.
In den Bereichen, in denen f‘ positiv ist, ist die Funktion f monoton steigend. Dort nehmen die Funktionswerte also nach rechts hin zu.
Die mittlere Änderung zwischen zwei Punkten erhältst du mit dem Steigungsdreieck.
Die momentane Änderung an einem Punkt ist die erste Ableitung bei diesem x.
Kurvendiskussion
Schnittpunkte und Nullstellen
Für Schnittpunkte setzt du die zwei Funktionen gleich und löst nach x auf.
Für Nullstellen setzt du die Funktion gleich Null und löst nach x auf. Dabei kommen oft die pq-Formel oder der Satz vom Nullprodukt zum Einsatz. Hier findest du eine Playlist mit Videos zum Thema Nullstellen.
In manchen Fällen sollst du die Anzahl von Schnittpunkten zwischen einer rationalen Funktion und einer Geraden in Abhängigkeit von der Steigung der Geraden angeben. Dafür legst du am besten dein Geodreieck oder ein transparentes Lineal auf die Abbildung und probierst verschiedene Steigungen aus.
Flächen und Integrale
Wenn ein Integral über f von a nach b gefragt ist, achte darauf, ob du einen Graphen der Stammfunktion F vor dir hast. Dann brauchst du die Werte F(b) und F(a) nur abzulesen.
\int\limits_{a}^bf(x)dx=F(b)-F(a)Oft sollst du auch in einer Abbildung „Kästchen zählen“ oder Figuren wie Dreiecke, Rechtecke oder Trapeze finden, mit deren Hilfe du Flächen unter einer Geraden berechnest.
Ableitungen und besondere Punkte im Graphen
Die Ableitung an einer Stelle x entspricht der Steigung der Tangente an diesem Punkt. Wenn du zu einer Abbildung eine Steigung angeben sollst, kann eine Lösung das Einzeichnen einer Tangente sein. In diesem Fall hast du für den Wert einen gewissen Spielraum, weil das Anlegen des Geodreiecks auf dem Augenmaß basiert.
Es kam allerdings auch vor, dass in einer Abbildung sowohl f als auch f‘ zu sehen waren. In diesem Fall sollte f'(x) direkt abgelesen werden.
Folgende Tabellen zeigen wichtige Zusammenhänge zwischen Funktionen, ihren Ableitungen und Stammfunktionen:
| Symbol | Bedeutung |
|---|---|
| F(x) | Stammfunktion, Fläche zwischen f und x-Achse |
| f(x) | Funktion, y-Koordinaten aller Punkte |
| f'(x) | Ableitung, Steigung der Tangente an der Stelle x |
| f“(x) | zweite Ableitung, Krümmung der Kurve |
Die dritte Ableitung brauchen wir nur, um einen Wendepunkt zu überprüfen. Oft wird sie gar nicht verlangt.
Außerdem ist es wichtig, sich zu merken, dass die Funktion f(x) die Ableitung der Stammfunktion F(x) ist. Wenn du zeigen sollst, dass F eine Stammfunktion von f ist, dann leitest du F ab. Idealerweise sollte dabei als Ergebnis f herauskommen.
Wenn die Funktion f eine Geschwindigkeit darstellt, dann gibt ein Integral die Bestandsänderung an. Ein paar Beispiele:
Hat f die Einheit Meter pro Sekunde -> F gibt die gefahrene Strecke an
Ist f in L pro Minute angeben -> F gibt das zugeflossene Volumen an
Ist f eine Infektionsrate -> F ist die Anzahl der Infektionen im betrachteten Zeitraum
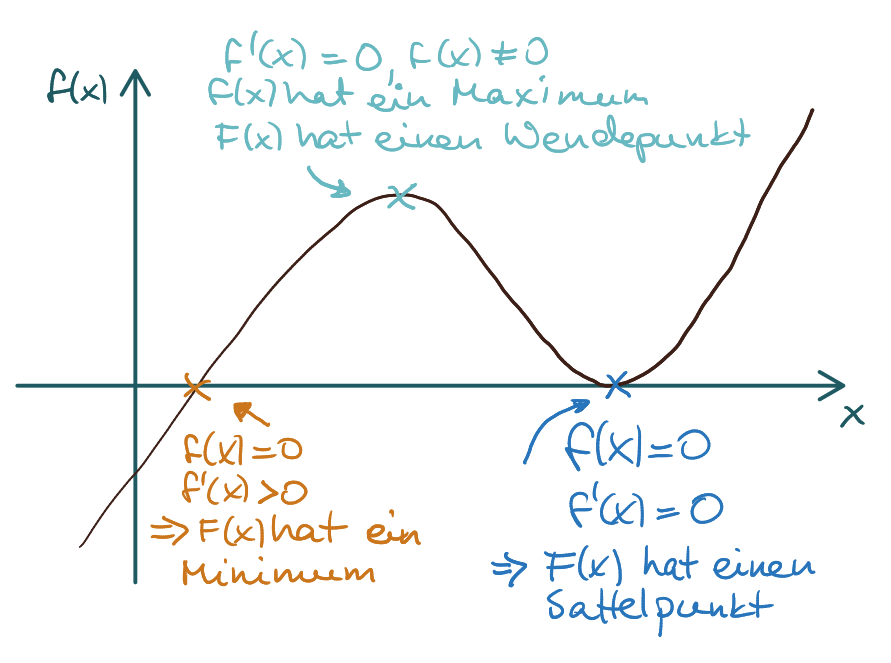
Für besondere Punkte im Graphen ist die folgende Tabelle hilfreich:
| F | Wendep. | Extremp. | Sattelp. | |||
| f | Wendep. | Extremp. | Nullst. | Sattelp. | Nullst. | |
| f‘ | Extremp. | Nullst. | k. Nullst. | Sattelp. | Nullst. | Nullst. |
| f“ | Nullst. | k. Nullst. | Nullst. | Nullst. | ||
| f“‘ | k. Nullst. | Nullst. |
Wenn also zum Beispiel die Funktion f eine Nullstelle hat, die erste Ableitung f‘ aber nicht, dann hat die Stammfunktion einen Extrempunkt.
Wenn die Funktion f und die erste Ableitung beide jeweils eine Nullstelle haben, dann hat die Stammfunktion bei diesem x einen Sattelpunkt.
Auch der hilfsmittelfreie Teil im Mathe-Abi erfordert immer wieder die Produktregel und die Kettenregel zum Ableiten.
Symmetrie
Für die Bestimmung der Symmetrie setzt du -x statt x in eine Funktion ein und vereinfachst den Funktionsterm.
Wenn am Ende f(-x) = f(x) herauskommt, ist die Funktion achsensymmetrisch..
Wenn stattdessen f(-x) = -f(x) herauskommt, ist die Funktion punktsymmetrisch.
In allen anderen Fällen ist sie nicht symmetrisch. Stell dich darauf ein, dass Fragen dieser Art vorkommen:
h(x) ist punktsymmetrisch, g(x) ist achsensymmetrisch. Welche Symmetrie hat f(x) = (h(x))2 · g(x)?
Dafür setzt du -x ein:
g(-x) = g(x) und h(-x) = -h(-x)
f(-x) = (h(-x))2 · g(-x)
= (-h(x))2 · g(x)
= (h(x))2 · g(x), denn Minus mal Minus ergibt Plus.
Also ist f(-x) = f(x) und damit ist f(x) achsensymmetrisch.
Skizzieren von Funktionen
Funktionen skizzieren
Um Funktionen zu skizzieren, gehe ich so vor:
- Bekannte Punkte und Nullstellen ankreuzen
- Hoch und Tiefpunkte mit einer kleinen „Schale“ andeuten
- Grenzwerte mit Pfeilen andeuten
- Bei rationalen Funktionen Wendepunkte zwischen Hoch- und Tiefpunkten andeuten, dabei schon den Wechsel zwischen Rechts- und Linkskurve (beziehungsweise anders herum) anpeilen.
- Bei e-Funktionen Wendepunkte zwischen Hochpunkt und Asymptote andeuten, dabei Wechsel der Krümmung anpeilen.

- Beherzt eine Linie durch diese Elemente ziehen:
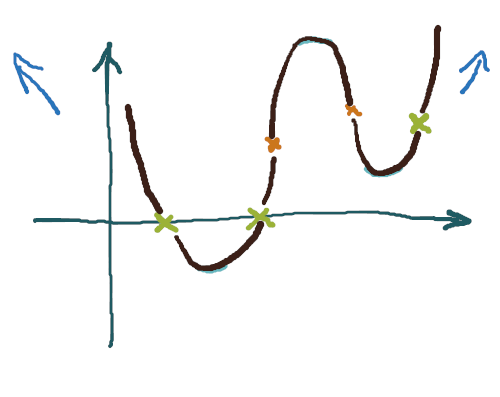
Auf diese Weise werden Extrempunkte nicht zu spitz und die Wendepunkte sitzen korrekt. außerdem lässt sich so der Graph auch sehr viel leichter zeichnen. Es geht bei diesen Skizzen nicht um Schönheit, sondern um Richtigkeit 🙂
Transformation von Graphen
Spiegeln an der y-Achse:
g(x) = f(-x)
-> Du setzt also überall, wo ein x vorkommt, stattdessen (-x) ein.
Spiegeln an der x-Achse:
g(x) = -f(x)
-> Du multiplizierst also einfach die Funktion mit -1. Vorne und hinten eine Klammer und ein Minus davor gesetzt.
Verschiebung senkrecht
Zum Beispiel um 5 nach oben:
g(x) = f(x) + 5
-> Du addierst also am Ende zu f(x) 5 dazu.
Verschiebung waagerecht
Zum Beispiel um 2 nach rechts:
g(x) = f(x-2)
-> Du setzt also überall, wo ein x vorkommt, stattdessen (x-2) ein.
Spiegeln an einer beliebigen senkrechten Achse
Zum Beispiel x = 2
Du spiegelst die Funktion zunächst an der y-Achse und schiebst sie dann um 2 nach rechts:
g(x) = f(-x-2)
-> Du setzt also überall, wo ein x vorkommt, stattdessen (-x-2) ein.
Spiegeln an einer beliebigen waagerechten Achse
Zum Beispiel y = -1
Du spiegelst die Funktion zunächst an der x-Achse und schiebst sie dann um 1 nach unten:
g(x) = -f(x)-1
-> Du multiplizierst also die Funktion mit -1 und ziehst danach 1 ab. Vorne und hinten eine Klammer, ein Minus davor gesetzt und danach noch -1 dahinter geschrieben.
Streckung/ Stauchung entlang der y-Achse
g(x)=a · f(x)
-> Du multiplizierst f(x) mit dem gewünschten Faktor. Vorne und hinten eine Klammer und das a davor geschrieben.
Stauchung/Streckung entlang der x-Achse
g(x) = f(b·x)
-> Du setzt also überall, wo ein x vorkommt, stattdessen (b·x) ein. Je größer b, umso stärker wird die Funktion zieharmonikamäßig zusammen geschoben. Bei kleinem b wird der Graph auseinander gezogen.
Du kannst einen Teil dieser Transformationen in dieser Geogebraseite mit Schiebereglern ausprobieren.
Koordinaten eines Punktes nach der Transformation
Wenn du angeben sollst, wo ein Punkt nach dieser Transformation landet, berechnest du den Funktionswert g(x). Ein Beispiel:
f(x) = x2 + 2x – 4
g(x) soll durch Spiegelung an der x- Achse und Verschiebung um 1 nach unten entstehen:
g(x) = -(x2 + 2x – 4) – 1 = – x2 – 2x + 3
Aus dem Punkt P(3 | 11) wird der Punkt P'(3 | -12). Achte darauf, dass bei der Spiegelung an der x-Achse aus Hochpunkten Tiefpunkte werden und umgekehrt!
Die folgenden Punkte kamen nur vereinzelt vor, sind allerdings für das Verständnis grundlegender Konzepte wichtig:
Steckbriefaufgaben
Die Steckbriefaufgaben im HMF-Teil sind vom Aufwand her sehr übersichtlich. Das Vorgehen ist wie gehabt:
- Stelle die Funktion mit Parametern auf, zum Beispiel a·eb·x oder a·x2 + b
- Entnimm dem Text die Informationen für besondere Punkte.
- Stelle auf dieser Basis dein Gleichungssystem auf und löse es.
Verkettung von Funktionen
Rechne damit, dass Aufgaben des folgenden Typs vorkommen werden:
Berechnen Sie für f(x)= eg(x) die Steigung der Tangente an der Stelle x = 1.
Bei dieser Aufgabe war ansonsten nichts gegeben, außer einer Abbildung von g und g‘. Daraus ließen sich g(1) = 0 und g'(x) = 2 ablesen.
Mit Hilfe der Kettenregel ergibt sich:
f'(1) = g'(1) · eg(1) =2 · e0 = 2
Funktionstypen
Rationale Funktionen
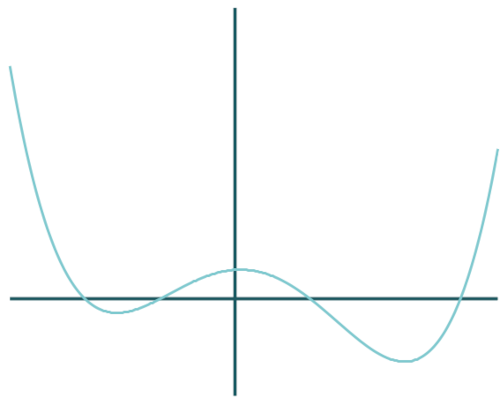
Dir sollte klar sein, dass am Grad einer Funktion ihr Aussehen ablesbar ist. Zum Beispiel hat eine Funktion dritten Grades maximal drei Nullstellen, maximal zwei Extrempunkte und in dem Fall einen Wendepunkt zwischen den Extrempunkten.
e-Funktionen
Hier sollte dir hauptsächlich klar sein, dass die Ableitung wieder die e-Funktion ist. Ausdrücke wie e2 oder ln(4) sind nicht im Kopf berechenbar und werden so stehen gelassen. e0 ist aber gleich Eins!
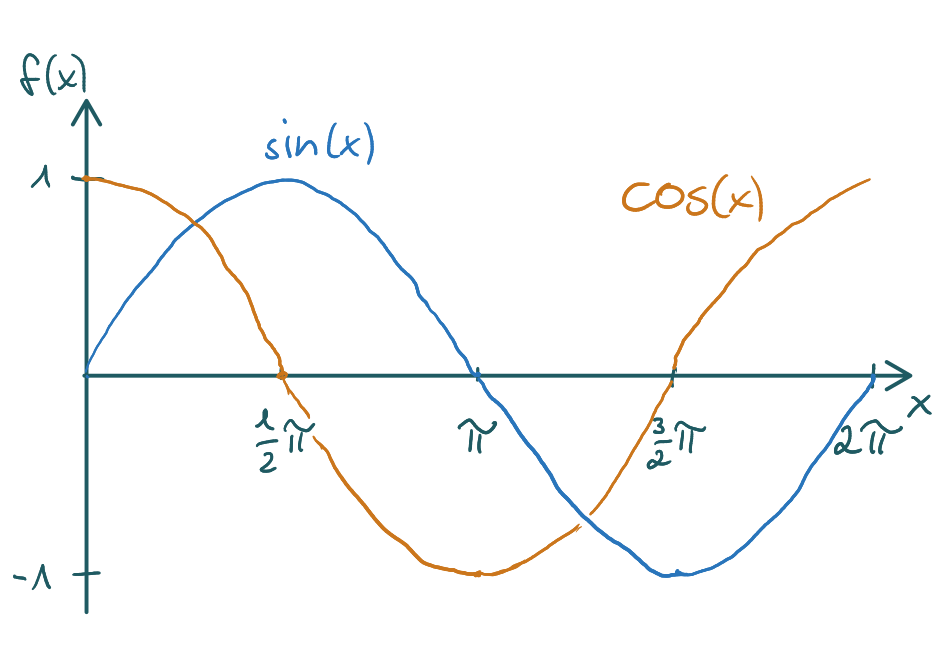
Sinus/Kosinus/Tangens
Du solltest eine ungefähre Vorstellung vom Aussehen der Graphen der Sinus- und Kosinusfunktion haben. Die y- Werte schwingen zwischen 1 und -1 hin und her. Wenn du eine x-Achse zwischen Null und π skizzierst, sehen die beiden Graphen so aus wie in der Abbildung oben.
Diese Skizze hilft dir dabei, dir wichtige Punkte zu merken. Ansonsten sollte klar sein, dass beide Funktionen links und rechts unendlich weiter verlaufen und dass die Ableitungen in folgender Reihenfolge laufen:
sin -> cos -> -sin -> -cos -> sin
Die Stammfunktionen verlaufen in der umgekehrten Reihenfolge.
In der Aufgabengruppe 2 kamen kompliziertere Fragen vor. Zur Lösung dieser Aufgaben musst du wissen, dass die Amplitude a, Periode b, die waagerechte Verschiebung c und die senkrechte Verschiebung d im Sinus und Kosinus folgendermaßen erscheinen:
f(x)=a\cdot sin\bigg(\frac{2\pi}{b}\cdot x-c\bigg)+d\\\quad\\f(x)=a\cdot cos\bigg(\frac{2\pi}{b}\cdot x-c\bigg)+dDen Tangens brauchst du zum Berechnen von Steigungswinkeln, denn
tan{x}=f'(x)Im hilfsmittelfreien Teil im Mathe-Abi lässt du Ausdrücke wie tan(3), die nicht im Kopf berechenbar sind, einfach so stehen.
Stochastik

Oft sind Zufallsgrößen vordefiniert. Wenn es mehrere Zufallsgrößen auf einem Aufgabenzettel gibt, ist es besonders wichtig, darauf zu achten, welche gerade gemeint ist.
Zum Beispiel kann im Einleitungstext stehen: „Die Zufallsgröße X ist binomialverteilt mit n = 50 und p = 0,2. Die Zufallsgröße Y beschreibt das Produkt aus zwei hintereinander gewürfelten Zahlen.“ Wenn du später aus verschiedenen Balkendiagrammen das passende heraus suchen sollst, macht es natürlich einen Unterschied, ob es um X oder um Y geht.
Insgesamt enthält die Stochastik viele Spielbeschreibungen und logisches Denken. Wie so oft empfehle ich immer eine Skizze 😉 Stell dich auch darauf ein, dass du dir anhand eines Terms für die Wahrscheinlichkeit eines Ereignisses eine dazu passende Spielsituation ausdenken sollst.
Ein weiterer wichtiger Punkt: Wenn bei einem Glücksspiel eine Zeitlang unerwartet oft ein bestimmtes Ergebnis aufgetreten ist, sagt das nichts über die kommenden Versuche aus. Wir Menschen neigen zu Aussagen wie „Jetzt habe ich so lange keine Sechs gewürfelt, da muss jetzt bald eine kommen.“ Von dir wird erwartet, dass du formulierst, dass so eine Art zu denken nicht der Wirklichkeit entspricht.
Zufallsexperimente
Baumdiagramme
Oft ist die Aufgabe, ein Baumdiagramm zu zeichnen. In anderen Fällen ist es extrem hilfreich, ein Baumdiagramm zu zeichnen, um die Wahrscheinlichkeit für ein komplizierteres Ereignis zu berechnen.
Denke daran, entlang der Pfade die Wahrscheinlichkeiten zu multiplizieren und quer zu den Pfaden zu addieren.
Bevor du das Baumdiagramm beschriftest, stelle noch einmal klar, ob zurückgelegt wird oder nicht und wie das die Wahrscheinlichkeiten beeinflusst.
Wenn du die Wahrscheinlichkeit für ein Ereignis nicht kennst, beschrifte den entsprechenden Zweig im Diagramm mit einem p.
Wenn oft gewürfelt oder gezogen wird, ist der Baum zu groß, um ihn komplett zu zeichnen. Dann empfehle ich, nur den Pfad zu zeichnen, der die geforderte Geschichte wiedergibt.
Beispiel: „Zehn Überraschungseier werden nacheinander zufällig ausgewählt. Geben Sie einen Term zur Berechnung der Wahrscheinlichkeit dafür an, dass nur in den letzten beiden Überraschungseiern jeweils eine Figur enthalten ist.“
Hier würde ich einen Pfad zeichnen,der achtmal nach links und zweimal nach rechts abzweigt. Die Skizze ist nur für dich und muss nicht vollständig sein.
Wahrscheinlichkeit für ein komplexes Ereignis
In manchen Fällen hilft ein Baumdiagramm, zum Beispiel, wenn zunächst eine von drei Urnen und dann daraus eine Kugel gezogen wird.
In anderen Fällen berechnest du die Anzahl der Möglichkeiten, die eine bestimmte Bedingung erfüllen und teilst sie durch die Anzahl aller Möglichkeiten. Manchmal brauchst du dafür die Formeln aus der Kombinatorik, manchmal hilft eine Tabelle.
Beispiel:
Wie groß ist die Wahrscheinlichkeit, bei zweimaligem Würfeln die Augensumme 5 zu erhalten.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
In der ersten Zeile und der ersten Spalte sind in orange die Augen des ersten bzw zweiten Würfels angegeben. In den übrigen Feldern die Augensummen.
Aus der Tabelle ist zu entnehmen, dass es vier Möglichkeiten für die Augensumme 5 gibt und insgesamt 36 mögliche Ergebnisse. Damit ist die Wahrscheinlichkeit 5:36.
Wenn die Wahrscheinlichkeit für ein Ereignis berechnet werden soll, das sich aus zwei Ereignissen zusammensetzt, musst du die Einzelwahrscheinlichkeiten berechnen und addieren. Es sei denn, die Ereignisse überlappen wie in diesem Beispiel:
A: Bei zweimaligem Würfeln fallen nur gerade Zahlen
A=\{2\vert 2,2\vert 4,\boxed{2\vert 6},4\vert 2,\boxed{4\vert 4},4\vert 6,\boxed{6\vert 2},6\vert 4,6\vert 6\}\\\quad \\ \implies P(A)=\frac{9}{36}B: Bei zweimaligem Würfeln ist die Augensumme 8
B=\{\boxed{2\vert 6},3\vert 5,\boxed{4\vert 4},5\vert 3,\boxed{6\vert 2}\}\\\quad\\ \implies P(A)=\frac{9}{36}Die Schnittmenge „A und B“ enthält drei Elemente.
\footnotesize{A\cup B=}\\\quad\\\footnotesize{\{\boxed{2\vert 6},\boxed{4\vert 4},\boxed{6\vert 2}\}}P(A\cup B)=P(A)+P(B)-P(A\cap B)\\\quad\\ =\frac{9}{36}+\frac{5}{36}-\frac{3}{36}=\frac{11}{36}Denn für P(„A oder B“) dürfen wir die Kombinationen in den Kästchen nicht doppelt zählen.
\footnotesize{A\cup B=}\\\quad\\\footnotesize{\{2\vert 2,2\vert 4,\boxed{2\vert 6},3\vert 5,4\vert 2,\boxed{4\vert 4},4\vert 6, 5\vert 3,\boxed{6\vert 2},6\vert 4,6\vert 6\}}Urnenaufgabe
Dieser Aufgabentyp ist so populär, weil sich damit so viele Geschichten erzählen lassen. In den Aufgaben der letzten Jahre wurden regelmäßig verschiedene Urnen mit unterschiedlich vielen verschiedenfarbigen Kugeln bestückt.
Teils wurden dann Kugeln zwischen den Urnen hin und her getauscht, teils wurde zufällig eine der Urnen gewählt. Am Ende stand meist die Frage, mit welcher Wahrscheinlichkeit eine Kugel einer bestimmten Farbe gezogen würde.
Bei solchen Geschichten ist ein Baumdiagramm hilfreich, an dem du die zeitliche Abfolge der Schritte ordentlich auflistest. Bei der zufälligen Wahl von Urnen ist die Wahrscheinlichkeit 1 geteilt durch die Anzahl der Urnen.
Für andere Geschichten war der Anteil der Kugeln in der gesuchten Farbe unbekannt und musste aus der Wahrscheinlichkeit eines bestimmten Ereignisses geschlossen werden. Auch hier hilft ein Baumdiagramm, an dem du den Anteil erst einmal als p einträgst.
Stochastische Unabhängigkeit
Wenn A und B stochastisch unabhängig sind, gilt:
P_A(B)=\frac{P(A\cap B)}{P{A}}=P(B)Um das zu prüfen, helfen dir ein Baumdiagramm oder eine Vierfeldertafel.
Wahrscheinlichkeitsverteilungen
Erwartungswert bei einer willkürlichen Verteilung, faires Spiel
E(X) ergibt sich, wenn du alle Werte, die die Zufallsgröße X annehmen kann mit der jeweils dazu gehörenden Wahrscheinlichkeit multiplizierst und dann alle Ergebnisse zusammen addierst.
Ich empfehle, falls nicht schon gegeben, eine Tabelle aufzustellen und die einzelnen Summanden dann unter die jeweiligen Spalten zu schreiben.
| X | 10 | 20 | – 8 |
| P(X) | 0,1 | 0,05 | 0,85 |
| X · P(X) | 1 | 1 | – 6,8 |
Wäre dies ein Spiel, wäre der Erwartungswert für den Gewinn
E(X) = 1 € + 1 € – 6,80 € = – 4,80 €
Es kann also davon ausgegangen werden, bei jedem Spiel durchschnittlich 4,80 € zu verlieren.
In diesem Zusammenhang wird oft nach einem fairen Spiel gefragt, oder nach dem Einsatz, bei dem sich „auf lange Sicht“ die Einsätze und Auszahlungen ausgleichen. Dafür berechnest du den Erwartungswert für die Auszahlung. Für ein faires Spiel muss der Einsatz genau diesem Wert entsprechen.
Term im Sachzusammenhang interpretieren
Immer wieder sollst du einen Term interpretieren, der folgende Form hat:
{20 \choose 1}\cdot 0,2\cdot0,8^{19} Dabei handelt es sich um die Bernoulliformel. Weil sie im HMF-Teil vorkommst, solltest du sie auswendig können.
P(X=k)={n \choose k}\cdot p^k\cdot(1-p)^{n-k} Aus den Exponenten und dem ersten Faktor kannst du n = 20 und k = 1 ablesen. Diese beziehen sich meistens auf eine Situation, die im Aufgabentext beschrieben wurde.
Aus dem zweiten und dritten Faktor kannst du die Trefferwahrscheinlichkeit p = 0,2 ablesen.
Die drei Werte n, p und k musst du dann noch auf die Geschichte beziehen, die der Aufgabe zugrunde liegt.
Wichtig zu wissen ist auch:
{n \choose 0}={n \choose n}=1\\\quad\\ {n \choose 1}=n\quad\quad (1-p)^0=1Wenn k = 1 ist, dann ist der vordere Faktor also nur eine Zahl, diese ist dann n.
In anderen Fällen sieht ein Term ungefähr so aus:
\bigg(\frac{2}{5}\bigg)^7Hier wurde ein Experiment siebenmal wiederholt und jedesmal dasselbe Ergebnis mit der Trefferwahrscheinlichkeit von 2/5 beobachtet. Hier ist n = k = 7 und daher sind der erste und der dritte Faktor der Bernoulliformel 1. Und in einem Produkt kann der Faktor 1 weggelassen werden.
Glücksradaufgabe
Bei diesem Aufgabentyp ist wichtig, dass der Winkel über einen Dreisatz mit der Wahrscheinlichkeit zusammenhängt.
360° entsprechen 100 %. Ist dein Winkel gegeben, zum Beispiel φ = 72°, dann gehört zu diesem Feld auf dem Glücksrad die Wahrscheinlichkeit 72° : 360° · 100 % = 20 %
Es kommt vor, dass der Winkel zunächst nicht gegeben ist, dann lässt du die Wahrscheinlichkeit als p = φ : 360° stehen.
Manchmal wird der Winkel im Bogenmaß betrachtet, dann gilt: 2π entspricht 100 %.
Binomialverteilung, Bernoulliformel
Da du die Formelsammlung im HMF-Teil nicht zur Verfügung hast, musst du dir die Bernoulliformel auswendig merken:
P(X=k)={n \choose k}\cdot p^k\cdot(1-p)^{n-k} Das n gibt die Anzahl der Wiederholungen an, das k die Anzahl der Treffer und das p die Trefferwahrscheinlichkeit. Insgesamt berechnest du so die Wahrscheinlichkeit für genau k Treffer.
Besondere Binomialkoeffizienten sind diese hier:
{n \choose 0}={n \choose n}=1\quad\quad {n \choose 1}=nDamit du annehmen kannst, dass eine Binomialverteilung vorliegt, kannst, muss das p bei jeder Wiederholung immer gleich sein. Es muss also zum Beispiel beim Ziehen aus einer Urne die Kugel jeweils wieder zurück gelegt werden.
Immer wieder sollen einer Geschichte Balkendiagramme zugeordnet werden. Dafür siehst du dir die x-Achse an, ob überhaupt n Balken angezeigt werden. Wenn es mehr als n Balken sind, passt das Diagramm nicht zu der Geschichte.
Dann rechnest du mit n·p den Erwartungswert µ aus. Bei diesem Wert muss im Diagramm das Maximum sein.
Ansonsten hilft es noch, die Höhen der Balken zusammenzuzählen. Dabei muss 1 heraus kommen, ansonsten zeigt das Diagramm keine Wahrscheinlichkeitsverteilung.
Die Standardabweichung σ berechnest du so:
\sigma=\sqrt{n\cdot p\cdot (1-p)}Wenn dieser Wert größer ist als drei, kann die Binomialverteilung näherungsweise als normalverteilt behandelt werden.
Auch wenn du für kumulierte Wahrscheinlichkeiten den Taschenrechner nicht verwenden kannst, kommt es vor, dass du sie dir logisch zusammenreimen sollst:
Wenn zum Beispiel p = 0,5 ist, dann ist die Verteilung symmetrisch. Ist zusätzlich noch zum Beispiel gegeben, dass bei n = 100 die Wahrscheinlichkeit P(X<20) = 0,05 ist, dann ist auch die Wahrscheinlichkeit P(X>80)= 0,05 und damit bleibt für ein eventuell gefragtes Intervall von 20 bis 80 noch 0,9 übrig.
In einer Aufgabe war die Verteilung nicht als gewohntes Balkendiagramm präsentiert, sondern in „kumulierten Werten“. Jeder Balken hat die Höhe P(X=k) plus die Höhe des Balkens links daneben. Der letzte Balken hat also die Höhe 1. Der Wert P(X=k) für ein beliebiges k kann berechnet werden, indem von dem jeweiligen Balken der Balken des linken Nachbarn abgezogen wird.
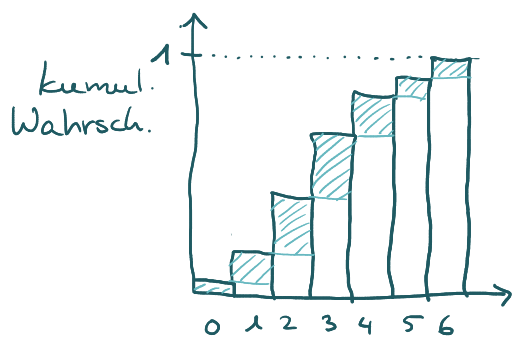
In diesem Bild entsprechen die türkis schraffierten Flächen jeweils den Wahrscheinlichkeiten P(X=k).
„Dichtefunktion“
Dieser Ausdruck sollte dich nicht erschrecken. Es geht in diesen Aufgaben nur um eine Normalverteilung. Oft ist die Glockenkurve abgebildet, in der du eine Fläche einzeichnen sollst, also die Wahrscheinlichkeit dafür abschätzen, dass der Wert der Zufallsgröße x in dem betrachteten Intervall liegt.
Merke: Die komplette Fläche unter der Kurve ist 1 oder 100%.
Wenn der Erwartungswert µ sich ändert und die Standardabweichung σ gleich bleibt, verschiebt sich die Glocke nach rechts oder links.
Wenn µ gleich bleibt und σ größer wird, bleibt das Maximum an der gleichen Stelle und die Glocke wird breiter und gleichzeitig flacher.
Kombinatorik
n und k identifizieren
Frage dich, ob bei dem Zählverfahren zurückgelegt wird oder nicht, ob die Reihenfolge wichtig ist oder nicht, und eventuell ob alles verteilt wird oder nicht.
n: Aus wie vielen Optionen kann ich für jede Ziehung wählen?
k: Wie oft ziehe ich?
Richtige Formel auswählen
Der größte Teil der Geschichten lässt sich auf folgende Grundmuster zurückführen:
Prinzip Zahlenschloss (mit Zurücklegen, mit Beachtung der Reihenfolge)
n^k
Prinzip Klassenphoto (ohne Zurücklegen, mit Beachtung der Reihenfolge, alle Kinder kommen mit auf das Photo)
n!
Prinzip Siegertreppchen (ohne Zurücklegen, mit Beachtung der Reihenfolge, nur ein Teil der Teilnehmenden kommen auf das Treppchen)
\frac{n!}{(n-k)!}Prinzip Weihnachtsmann, der mit einem Griff aus seinem Sack drei Geschenke für ein Kind zieht (ohne Zurücklegen, Reihenfolge egal, Hauptsache Geschenke 😉)
{n \choose k}Prinzip Blumenstrauß, bei dem n Blumen zusammen gebunden werden, wobei aus k Farben gewählt werden kann.
{{n+k-1} \choose {k-1}}Du musst in den meisten Fällen nur den Term aufschreiben und nicht fertig berechnen.
Vektoren
Obwohl Kreise für 2024 nicht bei allen meinen Schüler*innen behandelt wurden, gab es eine Kreisaufgabe, allerdings noch 2020, also bevor dieses Thema in Schleswig-Holstein gestrichen wurde. Es ist gut möglich, dass in Zukunft der hilfsmittelfreie Teil im Mathe-Abi wieder Kreisgleichungen enthalten wird, allerdings machte dieser Aufgabentyp von 2017 bis 2023 nur 4 % aller Aufgaben aus.
Du solltest grundsätzlich nach rechtwinkligen Dreiecken Ausschau halten und den Satz des Pythagoras auswendig wissen.
Im Folgenden bezeichnen bei Geradengleichungen die Begriffe Ortsvektor und Stützvektor dasselbe 🙂
Zurechtfinden im Koordinatenssytem
Koordinaten eines Punktes aus Text oder Abbildung erschließen
Ich sage es nochmal: Hier hilft eine Skizze extrem weiter 🙂 Falls du nicht schon eine Abbildung vorliegen hast. In der darfst du so viel herum malen wie nötig, um Dinge klarer zu sehen.
Jeder Punkt hat einen dazu gehörenden Ortsvektor. Die Koordinaten sind dieselben, nur um 90° „gekippt“.
Vektoraddition: Du überlegst dir, wie du über bekannte Punkte zum gesuchten Punkt kommst und addierst deine „Reisebeschreibung“ auf.
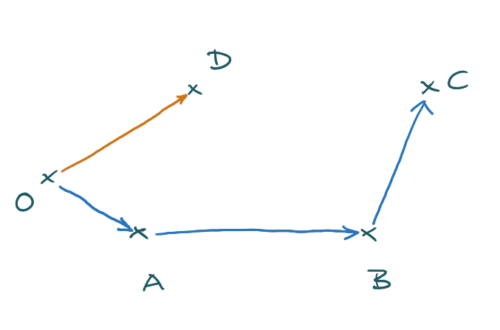
Wenn du zum Beispiel einen Punkt D bestimmen sollst, der zu einem Parallelogramm ABCD gehört und von dem du die Punkte A. B und C kennst, sieht diese Reise so aus, dass zu vom Ursprung erst zu A gehst und dann dort den Vektor von B nach C dran hängst.
\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{BC}Wenn du einen Punkt so bestimmen sollst, dass eine Figur einen vorgegebenen Flächeninhalt hat oder ein Körper ein gegebenes Volumen, setzt du für die Koordinaten erst einmal allgemein x, y und z ein. Dann berechnest du alle nötigen Vektoren. Im hmf-Teil sind viele Nullen dabei, sodass der Rechenaufwand gering ist. Am Ende setzt du den resultierenden Term mit der gegebenen Fläche beziehungsweise dem Volumen gleich.
Oft ergibt sich aus einer Skizze zu einer Pyramidenaufgabe auch, dass die Punkte der Bodenfläche alle auf der gleichen Höhe sind, zum Beispiel A ( 3 | 3 | 3 ) , B ( 6 | 7 | 3 ) und C ( 2 | 10 | 3 ). Wenn du dazu eine Spitze finden sollst, damit die Pyramide ein bestimmtes Volumen hat, berechnest du den Flächeninhalt der Grundseite.
Die Höhe der Pyramide ist
h=3\cdot V:G
Die z-Koordinate der Spitze muss in diesem Fall 3 + h sein. Die x- und y-Koordinaten sind frei wählbar.
Manchmal ergibt sich der Punkt aus dem Zusammentreffen mehrerer Bedingungen. Zum Beispiel könnte ein Punkt auf einer Geraden liegen und mit einem anderen Punkt einen Vektor bilden, der zu der Gerade senkrecht steht. Du ahnst es schon: Eine Skizze hilft 😉 Und hier das Konzept der Geradengleichung sowie das Skalarprodukt.
Rechter Winkel bei Skalarprodukt = 0
Weil das Skalarprodukt so einfach zu berechnen ist und der Nachweis von rechten Winkeln damit so leicht ist, kommen sehr viele Aufgaben zu diesem Zusammenhang vor.
Lerne, das Skalarprodukt und das Vektorprodukt auseinanderzuhalten. Für das Skalarprodukt multiplizierst du die Koordinaten der Vektoren miteinander und addierst die Ergebnisse. Am Ende bekommst du eine Zahl.
Term angeben
Es geht im hmf-Teil nicht darum, lange Berechnungen durchzuführen, sondern zu zeigen, dass du die Konzepte verstanden hast.
Deswegen lautet der Auftrag häufig:
Geben sie einen Term an, mit dem Sie berechnen könnten,…
Damit ist wirklich nur das gemeint. Du stellst hier zum Beispiel eine Vektoraddition auf und lässt sie so stehen.
Lage eines Punktes überprüfen
Immer wieder soll überprüft werden, ob ein Punkt auf einer Geraden oder einer Ebene liegt. Bei einer Ebene setzt du die Koordinaten ein und stellst fest, ob die Gleichung aufgeht.
Bei einer Geraden setzt du den Ortsvektor zum Punkt mit der Ebene gleich und löst das entstehende Gleichungssystem.
Das Ganze nennt sich Punktprobe.
Konzept Richtungsvektor
Während ein Ortsvektor immer vom Ursprung zu einem konkreten Punkt im Raum gedacht wird, ist ein Richtungsvektor frei im Raum verschiebbar. Er gibt an, wie du von einem beliebigen Punkt zu einem anderen Punkt kommst.
Einen Richtungsvektor berechnest du, indem du den Ortsvektor des Startpunktes vom Ortsvektor des Zielpunktes subtrahierst.
Richtungsvektor = Ende – Anfang
Diese Reihenfolge ist wichtig, weil anders herum der Vektor in die entgegengesetzte Richtung zeigt.
Konzept Koordinatenebenen
Die Gleichung für die xy-Ebene, beziehungsweise x1x2-Ebene lautet:
z = 0 bzw. x3=0
Normalenvektor
\overrightarrow{n}=\begin{pmatrix}0\\0\\1\end{pmatrix}Richtungsvektor 1
\overrightarrow{u}=\begin{pmatrix}1\\0\\0\end{pmatrix}Richtungsvektor 2
\overrightarrow{v}=\begin{pmatrix}0\\1\\0\end{pmatrix}Der Normalenvektor zeigt also in Richtung der z-Achse und die beiden Richtungsvektoren in Richtung der x- beziehungsweise der y-Achse. Für die anderen drei Ebenen musst du nur die Koordinaten tauschen.
Wenn ein Punkt in dieser Ebene liegen soll, muss er die z-Koordinate Null haben.
Wenn eine Gerade in dieser Ebene liegen soll, muss ihr Aufpunkt als z-Koordinate eine Null haben und als frei wählbarer Richtungsvektor wären jeweils u oder v geeignet, ansonsten auch alle anderen Vektoren, die eine Null als z-Koordinate haben..
Vektoren sind zur xy-Ebene parallel, wenn ihre z-Koordinate Null ist.
Objekte in ein Koordinatensystem einzeichnen
Wiederhole noch einmal das Vorgehen, wie du einen Punkt in ein Koordinatensystem mit drei Achsen einträgst. Zuerst gehst du den Wert der X-Koordinate nach vorne oder hinten, dann von diesem Punkt aus den wert der y-Koordinate nach rechts oder links und von dieser zweiten Zwischenstation aus den Wert der z-Koordinate nach oben oder unten.
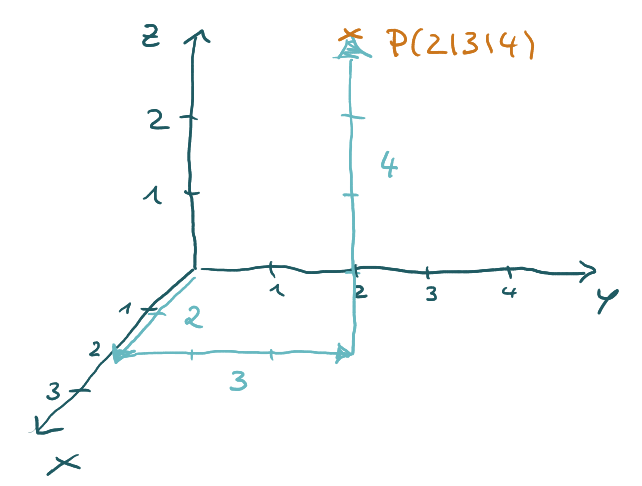
Geraden und Ebenen
Konzept Geradengleichung
Eine Geradengleichung setzt sich zusammen aus einem Ortsvektor zu einem Punkt auf der Geraden und einen Richtungsvektor, der zu der Gerade parallel ist.
Der Ortsvektor verankert die Gerade im Raum, der Richtungsvektor richtet sie aus.
Eine Gerade, deren Punkte immer drei gleiche Koordinaten haben ´, zum Beispiel P(4|4|4), hat folgende Gleichung:
g: \overrightarrow{x}=\lambda\cdot \begin{pmatrix}1\\1\\1\end{pmatrix}Der Aufpunkt ist im Ursprung, daher ist ein Ortsvektor nicht nötig und der Richtungsvektor addiert zu x, y, und z immer jeweils die gleiche Zahl dazu.
Wenn du eine Gerade angeben sollst, ist oft gefordert, dass sie durch einen speziellen Punkt geht und zu einer anderen Gerade parallel ist. Dann nimmst du diesen Punkt als Aufpunkt und den Vektor der anderen Geraden als Richtungsvektor.
Konzept Ebenengleichung
Der HMF-Teil im Mathe-Abi sieht für jedes Arbeitsblatt ungefähr 10 Minuten Bearbeitungszeit vor. Hier wird also nicht erwartet, dass du von Grund auf aus drei Punkten eine Ebene in Koordinatenform herbei zauberst
Möglich ist allerdings, dass zwei Geraden gegeben sind, die sich schneiden, und aus denen eine Ebene in Koordinatenform zusammengesetzt werden soll.
Dafür berechnest aus den beiden beteiligten Richtungsvektoren mit dem Vektorprodukt einen Normalenvektor und übernimmst den Stützvektor der einen Geraden. Daraus setzt du eine Ebenengleichung in Normalenform zusammen. Diese ausmultipliziert ergibt die Koordinatenform.
Gegebene Ebenen haben im hmf-Teil generell Koordinatenform. Richte dich darauf ein, dass du daran die Lage im Raum erkennen sollst, also den Normalenvektor ablesen und eventuell die Schnittpunkte mit den Koordinatenachsen berechnen.
Eine Ebene ist dann parallel zu einer der Koordinatenachsen, wenn die jeweilige Koordinate in der Ebenengleichung nicht vorkommt. Zum Beispiel ist E: 2y + 3z = 14 parallel zur x Achse. Du kannst das damit begründen, dass der Normalenvektor mit dem Vektor in Richtung der x-Achse das Skalarprodukt Null ergibt:
\begin{pmatrix}0\\2\\3\end{pmatrix}\circ \begin{pmatrix}1\\0\\0\end{pmatrix}= 0+0+0=0Konzept Normalenvektor
Der Normalenvektor steht auf einer Ebene senkrecht. Wenn du ihn berechnen sollst, dann nimmst du das Vektorprodukt aus zwei Richtungsvektoren, die in der Ebene liegen.
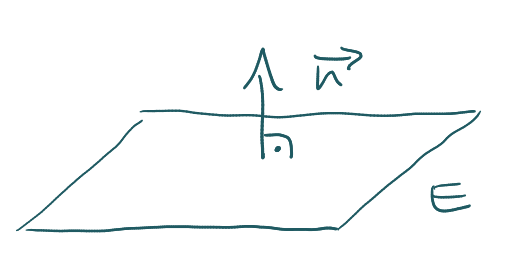
Oft kannst du aber auf den Richtungsvektor einer gegebenen Geraden zurückgreifen, die laut Aufgabentext auf der Ebene senkrecht steht. Du kennst es:
Mach dir eine Skizze.
Ebenen- und Geradenscharen
Was auch immer du an Lagebeziehungen zwischen Punkten, Geraden und Ebenen bestimmen kannst, kannst du auch mit Scharen machen. Wenn also in einem Vektor eine Koordinate keine Zahl, sondern ein Parameter (häufig ein a) ist, dann rechnest du das jeweilige Verfahren durch und behandelst das a wie eine Zahl.
Am Ende der Rechnung hast du dann einen Term oder eine Gleichung und musst überlegen, welches a die geforderte Bedingung erfüllt.
Beispiel:
Weisen Sie nach, dass g und ha für jeden Wert von a windschief sind.
g: \overrightarrow{x}=\begin{pmatrix}0\\1\\1\end{pmatrix}+\lambda\cdot \begin{pmatrix}1\\0\\-1\end{pmatrix}\\\quad\\g: \overrightarrow{h_a}=\begin{pmatrix}0\\0\\1\end{pmatrix}+\mu\cdot \begin{pmatrix}1\\a\\0\end{pmatrix}Wenn du die beiden Richtungsvektoren vergleichst, siehst du, dass sie unabhängig von a keine Vielfachen voneinander sein können.
Du setzt die beiden Geraden gleich und erhältst ein Gleichungssystem:
I \quad \lambda=\mu\\\quad\\II\quad1=\mu\cdot a\\\quad\\ III\quad 1-\lambda=1 \implies \lambda =0
Die dritte Gleichung sagt dir direkt, dass λ Null sein muss. Damit ist nach Gleichung I auch µ gleich Null. Daraus ergibt sich für Gleichung II, dass 1 = 0 · a ist.
Weil es kein a gibt, das diese Gleichung erfüllt, sind alle Geraden ha windschief zu g.
Lagebeziehungen
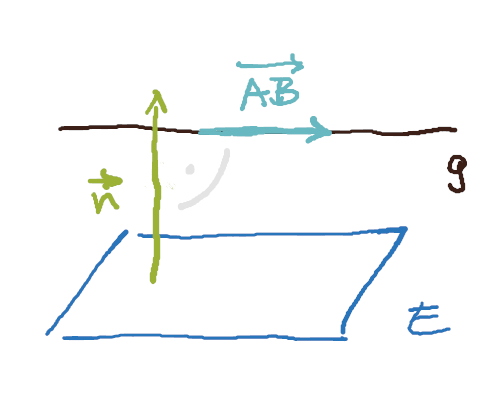
Gerade in einer Ebene oder parallel dazu
Wenn du zeigen sollst, dass eine Gerade in einer Ebene liegt, überprüfst du den Richtungsvektor der Geraden und den Normalenvektor der Ebene. Diese müssen senkrecht zueinander sein. Mit anderen Worten: Das Skalarprodukt muss 0 ergeben. Den Normalenvektor von E liest du an den Zahlen vor x, y und z direkt ab.
Beispiel
g: \overrightarrow{x}=\begin{pmatrix}0\\1\\1\end{pmatrix}+\lambda\cdot \begin{pmatrix}1\\0\\-1\end{pmatrix}\\\quad\\E: x+y+z=2 \implies \overrightarrow{n} = \begin{pmatrix}1\\1\\1\end{pmatrix}Das Skalarprodukt passt:
\begin{pmatrix}1\\0\\-1\end{pmatrix}\circ\begin{pmatrix}1\\1\\1\end{pmatrix}=1+0-1=0 \quad\checkmarkAußerdem muss der Aufpunkt der Geraden (ergibt sich aus dem Stützvektor)in der Ebene liegen. Dazu setzt du seine Koordinaten in die Ebenengleichung ein (Punktprobe):
0 + 1 + 1 = 2
Diese Gleichung stimmt auch, damit ist nachgewiesen, dass g in E liegt.
Soll die Gerade nur parallel zur Ebene sein, brauchst du die Punktprobe nicht.
Gerade schneidet Ebene
Bilde das Skalarprodukt aus dem Richtungsvektor der Geraden und dem Normalenvektor der Ebene. Wenn dabei nicht Null herauskommt, schneidet die Gerade die Ebene in einem Punkt.
Gerade schneidet Ebene senkrecht
Vergleiche den Richtungsvektor der Geraden und den Normalenvektor der Ebene. Sind sie parallel, steht die Gerade senkrecht auf der Ebene.
Zwei Geraden sind parallel zueinander
Vergleiche die Richtungsvektoren. Sie müssen parallel sein.
Zwei Geraden stehen senkrecht aufeinander
Bilde aus den Richtungsvektoren das Skalarprodukt. Es muss Null herauskommen.
Lineares Gleichungssystem
In den Jahren 2017 und 2023 gab es jeweils eine Aufgabe, die nur auf dem Lösen von linearen Gleichungssystemen basierte. Wenn du darauf vorbereitet sein willst, wiederhole am besten noch einmal das Additionsverfahren. Die Gleichungen enthielten relativ viele Nullen und Einsen, so dass der Rechenaufwand an sich gering war.
Wenn du am Ende Werte für alle Variablen bekommst, die alle Gleichungen erfüllen, hat das Gleichungssystem eine Lösung.
Kommt zwischenzeitlich etwas der Art 5 = 7 heraus, hat das Gleichungssystem keine Lösung.
Wenn irgendwann etwas der Art 5 = 5 herauskommt, hat das Gleichungssystem unendlich viele Lösungen.
Punkte
Abstand zwischen zwei Punkten
Du berechnest den Vektor zwischen den zwei Punkten. Aus dessen Koordinaten ergibt sich der Abstand über einen dreidimensionalen Pythagoras.
Beispiel:
A(2\vert4\vert2)\quad B(5\vert4\vert6)\quad\overrightarrow{AB}=\begin{pmatrix}3\\0\\4\end{pmatrix}\\\quad\\\vert\overrightarrow{AB}\vert=\sqrt{3^2+0^2+4^2}=5Schnittpunkte im HMF-Teil
Im hilfsmittelfreien Teil lohnt es sich oft, genauer hinzusehen, wenn der Schnittpunkt zweier Geraden gefragt ist. Oft steht in den Geradengleichungen jeweils der gleiche Stützvektor. Diese Aufgabe ist dann in unter einer Minute beantwortet, indem du nur diesen Stützvektor als Schnittpunkt angibst.
Sollten die beiden Stützvektoren tatsächlich unterschiedlich sein, setzt du die Geraden gleich und löst das entstehende Gleichungssystem.
Ebenen sind generell in der Koordinatenform angegeben. Den Schnittpunkt zwischen einer Ebene und einer Geraden erhältst du durch Einsetzen.
Bei der Frage, ob ein Schnittpunkt innerhalb einer definierten Fläche ist, hilft es, die Fläche und den Punkt in eine Koordinatensystem zu zeichnen.
Spurpunkte
Spurpunkte einer Ebene sind die Schnittpunkte mit den Koordinatenachsen. Für den Spurpunkt mit der x-Achse setzt du
y = 0 und z = 0
und berechnest dann x. Das ist deine x-Koordinate für den Spurpunkt. Für die anderen Achsen gehst du ähnlich vor, immer die beiden nicht gefragten Koordinaten werden gleich Null gesetzt.
Aus zwei Spurpunkten einer Ebene ergibt sich eine Spurgerade.
Spurpunkte einer Geraden sind die Schnittpunkte mit den Koordinatenebenen. Dafür setzt du die Geradengleichung gleich dem Ortsvektor, der an der passenden Stelle eine null hat. Beispielsweise könnte das das für die xz-Ebene so aussehen:
\begin{pmatrix}x\\0\\z\end{pmatrix}=\begin{pmatrix}2\\4\\-3\end{pmatrix}+\lambda\cdot \begin{pmatrix}1\\5\\-1\end{pmatrix}\implies\\\quad\\x=2+\lambda\\\quad\\0=4+5\lambda\\\quad\\z=-3-\lambdaDas entstehende Gleichungssystem löst du. Aus der zweiten Gleichung ergibt sich, dass λ = -0,8 ist. Das setzt du in die erste und dritte Geleichung ein.
Im hmf-Teil sind oft viele Nullen dazwischen. Hier ist es wenigstens eine in der zweiten Gleichung, sodass dieser Rechnungsschritt wenig Aufwand bedeutet. Es kann auch sein, dass du die obige Vektorgleichung nur aufstellen und nicht zu Ende rechnen musst. Das ergibt sich aus der Aufgabenformulierung.
Geometrische Berechnungen
Spiegelung an einer beliebigen Ebene
Immer wieder sollen Objekte an einer Ebene gespiegelt werden. Manchmal ist dafür wirklich eine Rechnung über ein Lotfußpunktverfahren nötig. Manchmal stellst du auch mit Hilfe einer Skizze fest, dass wieder einmal alles deutlich einfacher gemeint ist als es auf den ersten Blick klingt.
Beispiel:
Gegeben sind die Ebene E sowie die Punkt P, Q und S. S liegt in E, die Gerade durch P und Q steht senkrecht auf E und die Punkte P und Q haben den gleichen Abstand von der Ebene E.
Die Punkte S und P legen die Gerade g fest. Spiegelt man g an E, so erhält man die Gerade h. Geben Sie eine Gleichung von h an.
Das ist eine Menge Text. Ich empfehle, einmal kurz durchzuatmen und dann Schritt für Schritt daraus eine Skizze zu zeichnen:
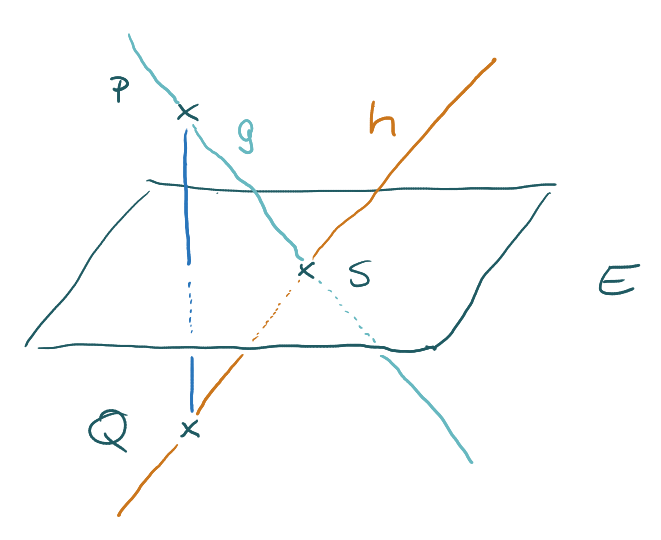
Wenn aus P durch Spiegelung Q wird und die Gerade g die Ebene in S schneidet, muss das Spiegelbild von g durch Q gehen. Damit kannst du einfach eine Gerade aus Q und S erzeugen.
In anderen Fällen war ein bisschen mehr Berechnung erforderlich. Ein Beispiel:
Gegeben sind der Punkt P und die Ebene E:
P(-1\vert7\vert2)\quad\quad E:x_1+3x_2=0
Bestimmen Sie die Koordinaten des Punktes Q, der entsteht, wenn P an E gespiegelt wird.
Als Skizze sieht das so aus:
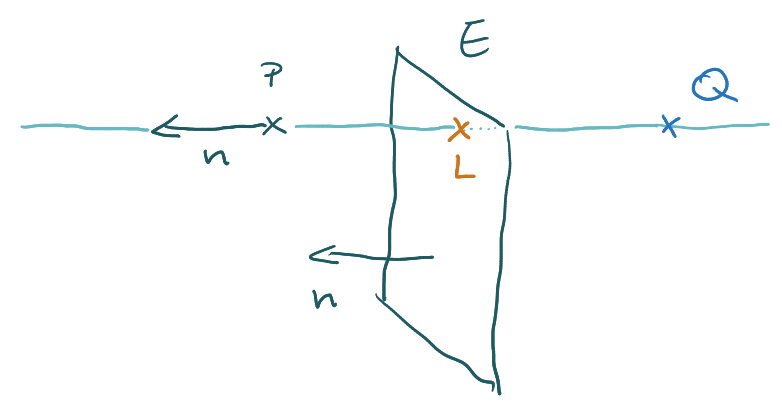
Mit dem Lotfußpunktverfahren findest du den Punkt L, der auf E und dabei mittig zwischen Q und P liegt. Dann brauchst du nur noch zweimal den Vektor zwischen P und L zu dem Ortsvektor von P zu addieren.
Umgekehrt gab es auch die Aufgabe, aus P und Q die Spiegelebene E zu ermitteln. Dabei ist der Vektor zwischen P und Q der Normalenvektor der Ebene, der Aufpunkt der Ebene ist L und liegt auf halber Strecke zwischen P und Q. Das heißt, du addierst zum Ortsvektor für P den halben Vektor zwischen P und Q. Mit diesen zwei Bausteinen setzt du die Normalenform der Ebene zusammen. Durch Ausmultiplizieren bekommst du die Koordinatenform.
Pyramidenvolumen
Das Volumen einer Dreieckspyramide ist ein Sechstel des Spatproduktes aus drei beteiligten Kantenvektoren.
Allerdings sind die hmf-Aufgaben auf eine Bearbeitungszeit von 10 Minuten pro Arbeitsblatt ausgelegt. Es ist daher sehr wahrscheinlich, dass das Volumen aus einer einfach zu berechnenden Grundfläche G und der aus der z-Koordinate abzulesenden Körperhöhe h berechnet werden soll:
V_{Pyramide}=\frac{1}{3}\cdot G\cdot hx3 bzw z als Höhe
Behalte im Hinterkopf, dass in Sachaufgaben, die sich um Gegenstände drehen, die z-Koordinate die Höhe eines Punktes im Raum ist. Das hilft oft bei der Orientierung, beim Skizzenbeschriften und beim Berechnen von Strecken oder Volumina.
Schattenwurf
Wegen der kurzen vorgesehenen Bearbeitungszeit kommen keine komplizierten Schattenwurfaufgaben vor. Grundsätzlich gehst du bei der Ermittlung eines Schattenpunktes so vor:
Punktförmige Lichtquelle:
Der Gegenstandspunkt ist der eine Punkt einer Geraden, die Lampe ist der andere Punkt. Die Gerade entspricht einem Lichtstrahl.
Sonnenbeleuchtung:
Die Richtung der Sonnenstrahlen ist vorgegeben. Dies ist der Richtungsvektor, der Gegenstandspunkt ist der Aufpunkt einer Geraden. Diese Gerade entspricht einem Sonnenstrahl.
Den Licht- beziehungsweise Sonnenstrahl schneidest du mit der Ebene, auf der der Schattenpunkt liegen soll.
Längenverhältnisse von Strecken, Streckenmittelpunkte
Zur Berechnung eines Streckenverhältnisses errechnest du die Längen der beiden Strecken und teilst sie durcheinander. Der größte Aufwand ist meistens die Ermittlung der Koordinaten des Punktes T, der eine Strecke AB in zwei Teile teilt.
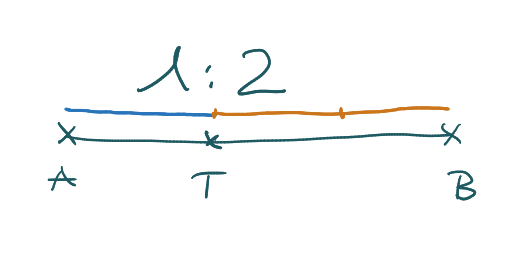
Wenn es sich dabei um den Streckenmittelpunkt handelt, sind beide Teilstrecken gleich lang.
Lotfußpunktverfahren
Wenn zwei Objekte „den kleinsten Abstand“ voneinander haben sollen, ist die senkrechte Verbindung gefragt. Dahinter steckt das Lotfußpunktverfahren.
Im Beispiel eines Punktes P und einer Ebene E nimmst du den Punkt P als Aufpunkt und den Normalenvektor n der Ebene als Bausteine für eine Gerade. Das ist die Lotgerade g. Schneidest du g mit E, ergibt sich der Lotfußpunkt L.
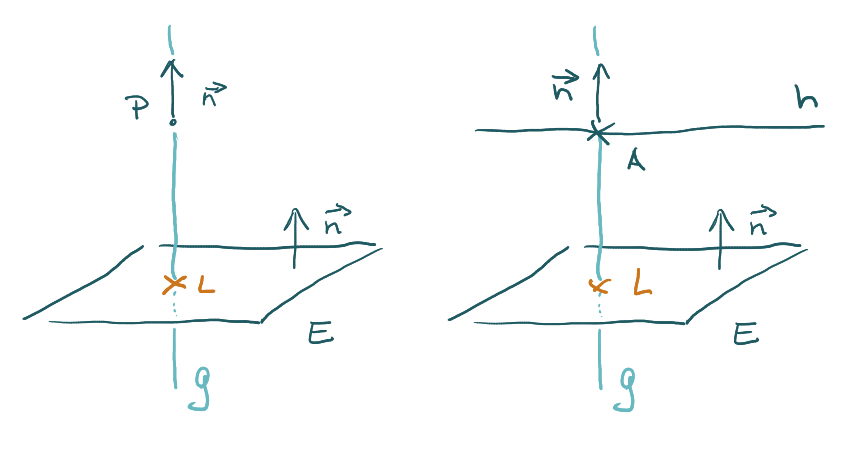
Im Beispiel einer Geraden h und einer Ebene E nimmst du als Aufpunkt der Lotgeraden den schon gegebenen Aufpunkt A der Geraden und als Richtungsvektor wieder den Normalenvektor n der Ebene. Am Ende ergibt sich wieder der Lotfußpunkt L.
Manchmal ist die Ebene E parallel zu einer der Koordinatenebenen, meistens zur xy-Ebene. Dann kann eine Aufgabe so lauten:
P liegt in E. Unter allen Punkten auf der Deckfläche F hat der Punkt S den kleinsten Abstand von P. E und F sind parallel zur xy-Ebene.
In einer Skizze sieht das Ganze so aus:
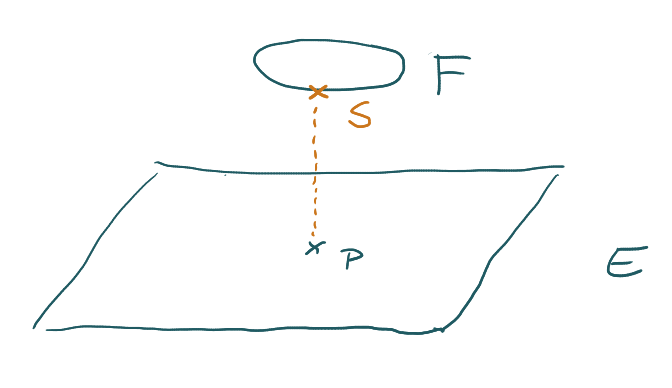
In diesem Fall haben P und S dieselben x- und y-Koordinaten. Die z-Koordinate von S ist die z-Koordinate der F-Ebene. Du musst also so gut wie nichts rechnen, wenn du dir die Zeit nimmst, eine schnelle Skizze anzufertigen.
Kreise
Du musst die Gleichung für einen Kreis nicht kennen, um zu wissen, dass alle Punkte auf der Kreislinie den gleichen Abstand vom Mittelpunkt M haben.
Sollte nachzuweisen sein, dass ein Punkt P auf einer Kreislinie, beziehungsweise auf der Kante der Grundfläche eines Zylinders liegt, dann berechnest du den Abstand des Punktes vom gegebenen Mittelpunkt. Dabei sollte der gegebene Radius r herauskommen.
Den Punkt Q genau gegenüber kannst du berechnen, indem du zum Ortsvektor von P zweimal den Vektor zwischen P und M addierst:
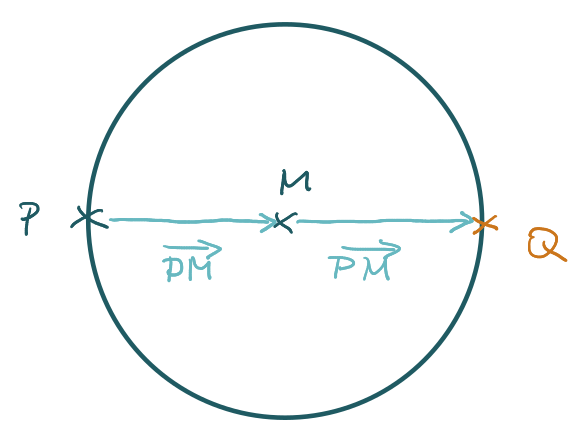
Matrizen
Diese Aufgaben wählt deine Schule nur aus, wenn ihr im Unterricht Matrizen behandelt habt. Wenn nicht, bekommt ihr entsprechend mehr Vektorrechnungsaufgaben.
Multiplikation
Dieses Video von MathemaTrick zeigt dir das Verfahren. Im Grunde ist besonders wichtig, dass du dir das Muster gut einprägst. Und dass du dich gut darauf konzentrierst, immer eine Zeile mit einer Spalte zu multiplizieren.
Stelle dich darauf ein, dass einige der Matrizen, die du mit anderen multiplizieren sollst, als Einträge Variablen statt Zahlen haben. Das könnte dann so aussehen:
\begin{pmatrix}0&0&3\\x&0&0\\0&0,7&0,8\end{pmatrix}\cdot\begin{pmatrix}0&0&3\\x&0&0\\0&0,7&0,8\end{pmatrix}\\\quad\\=\begin{pmatrix}0&0,21&0,24\\0&0&3x\\0,7x&0,56&0,64\end{pmatrix}Fehlende Einträge finden
In einigen Aufgaben waren die Einträge in Matrizen oder Vektoren Variablen statt Zahlen. Du rechnest mit diesen Variablen die verschiedenen Rechenverfahren bis zum Ende durch und durch Vergleichen mit einem gegebenen Vektor oder sonstigen Wert ergibt sich dann dass Ergebnis für die Variable.
Dabei kann es sich zum Beispiel um den Prozentanteil handeln, mit dem Jungtiere eines Wolfsrudels zu erwachsenen Tieren entwickeln.
Übergangsmatrix ↔ Übergangsdiagramm
Entweder ist eine Übergangsmatrix gegeben, die in ein Übergangsdiagramm umgewandelt werden soll, oder umgekehrt.
Von der Matrix zum Diagramm:
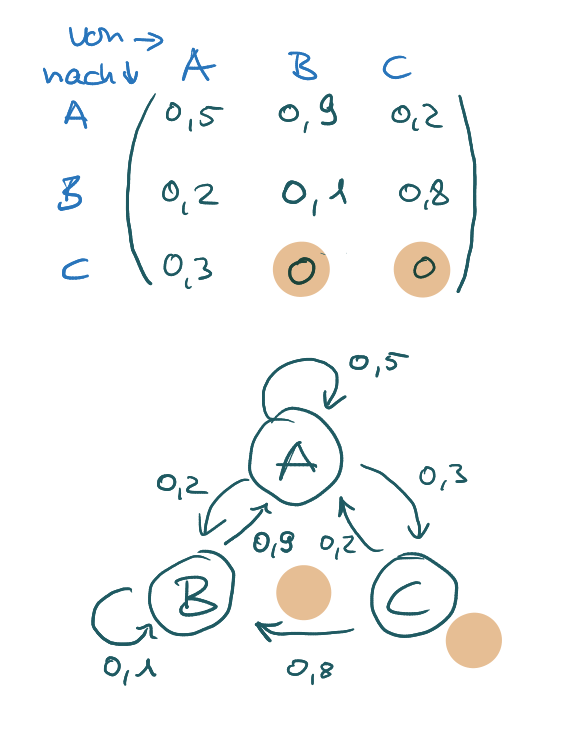
Ergänze die Matrix mit der Kopfzeile „von A, B, C“ und füge links eine Spalte „nach A, B, C“ zu. Zeichne drei Kreise, beschrifte sie mit A, B und C und verbinde sie mit Pfeilen. Schreibe die Werte an die Pfeile. Wenn ein Prozentanteil Null beträgt, lässt du den Pfeil weg.
Vom Diagramm zur Matrix:
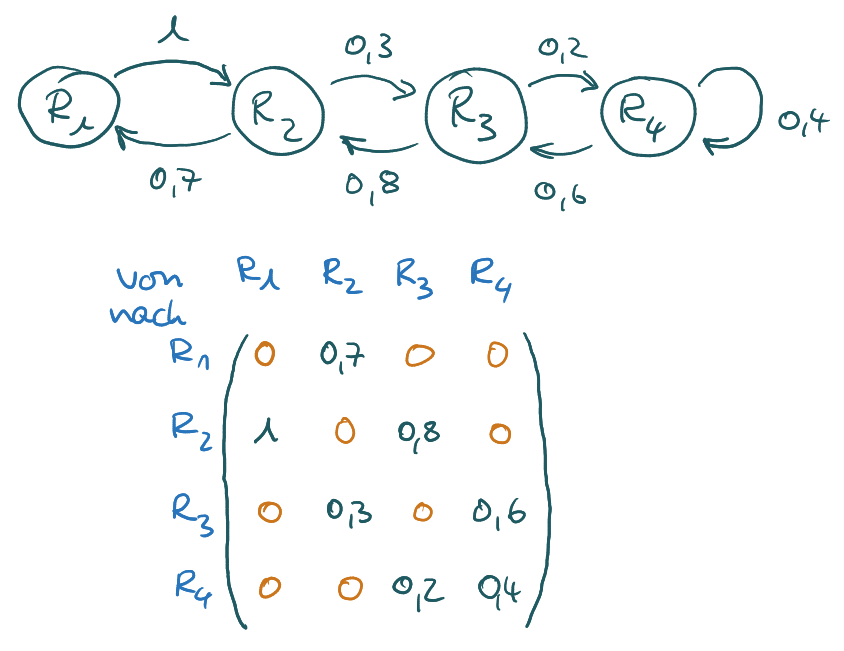
Schreibe dir eine von-nach Tabelle und übertrage alle Zahlen aus dem Diagramm. Fülle alle Lücken mit Nullen auf.
Bei Produktionsprozessen steht „von“ in der linken Spalte und „nach“ in der Kopfzeile, die Richtung ist also genau anders herum. Das Prinzip ist aber gleich.
Stationärer Vektor
Wenn die Zusammensetzung einer Population gefragt ist, „die sich im weiteren Verlauf nicht mehr ändert“, stellst du folgende Gleichung auf:
M\cdot \overrightarrow{v}=\overrightarrow{v}M ist hier die Übergangsmatrix und der Vektor v entspricht der Populationsverteilung.
Im hmf-Teil ist das entstehende Gleichungssystem generell eher übersichtlich. Manchmal ist auch schon die obige Gleichung als Arbeitsauftrag gegeben.
Es kann auch vorkommen, dass du diese Gleichung nur aufstellen und nicht fertig rechnen musst, um zu beschreiben, wie du den stationären Vektor herausfinden könntest.
Zahlen im Sachzusammenhang interpretieren
Oft ist die Frage, welche Bedeutung ein Eintrag in einer Übergangsmatrix im Sachzusammenhang hat.
In folgendem Beispiel legen Insekten Eier, aus denen Larven entstehen, die sich zu Insekten entwickeln:
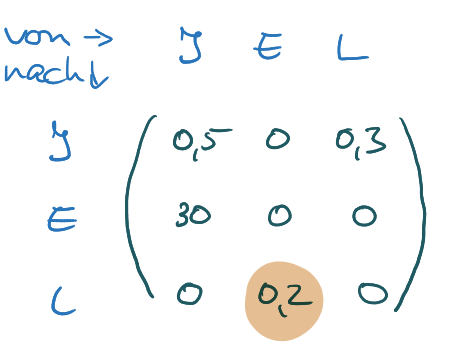
Du sollst erklären, was die 0,2 im Sachzusammenhang bedeutet. Die Antwort ist:
20% der Eier entwickeln sich innerhalb einer Zeiteinheit zu Larven.
Es sind unterschiedliche Geschichten, aber immer das gleiche Konzept „von -> nach“
Populationsentwicklungen beschreiben
Hier geht es darum, dass du dir logisch überlegst, was passiert, wenn zum Beispiel die Zahl der Schmetterlingseier das zehnfache der Zahl der Schmetterlinge vom Vorjahr ist, aus 80% der Eier erfolgreich Larven werden und aus 20% der Larven dann wieder Schmetterlinge.
Manchmal sollst du diese Überlegungen mit Diagrammen abgleichen, in denen der Verlauf der Populationszahlen mit der Zeit auf der x-Achse gezeigt wird. Dabei geht es meistens darum, ob die Population wächst oder schrumpft, ob sie stetig zunimmt oder schwankt.
In anderen Fällen sollst du beschreiben,wie sich die Verhältnisse in der Population ändern, dass also zum Beispiel der Anteil der Schmetterlingseier gegenüber den ausgewachsenen Schmetterlingen immer weiter zunimmt.
Inverse Matrizen
Inverse Matrizen verwendest du dazu, um aus einer aktuellen Population auf die vorherige Population zu schließen.
Für die Matrix M und die inverse Matrix M-1 gilt:
M\cdot M^{-1}=II ist die Einheitsmatrix, in der nur Einsen auf der Diagonalen von links oben nach rechts unten vorkommen und auf allen anderen Plätzen nur Nullen stehen.
Teils sind die inversen Matrizen schon gegeben, sodass du direkt mit ihnen rechnen kannst.
Teils sind inverse Matrizen selbst zu ermitteln. Dieses Video von MathemaTrick beschreibt das grundsätzliche Verfahren. Im hmf-Teil kommen allerdings eher 2×2-Matrizen mit ein paar Nullen als Einträge vor. Dann kannst du auch diesen Ansatz verwenden:
\begin{pmatrix}1&0\\-5&5\end{pmatrix}\cdot \begin{pmatrix}a&b\\c&d\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end{pmatrix}\\\quad\\\implies \begin{pmatrix}a&b\\-5a+5c&-5b+5d\end{pmatrix}=\begin{pmatrix}1&0\\0&1\end{pmatrix}\\\quad\\\implies a=1\quad b=0\quad c=1\quad d=0,2Hier sollst du die Inverse der linken Matrix heraus finden. Die Variablen a bis d sind die Platzhalter für die Einträge in der inversen Matrix. Du berechnest das Produkt aus M und M-1.
Durch Vergleich ergeben sich die Werte für a, b, c und d.
Ein paar Aufgabentypen kamen nur selten vor:
Produktionsmatrizen
Bei Produktionsmatrizen sind „von“ und „nach“ umgekehrt im Vergleich zu Populations-Übergangsmatrizen. Deswegen ergibt die Multiplikation der Matrix mit dem Vektor für die Produkte den Vektor für die Rohstoffe. Wir rechnen hier also zeitlich gesehen in die Vergangenheit.
„rückwärts“ rechnen
Wenn angegeben werden soll, wie die Verhältnisse in einer Population im letzten Jahr waren oder wie viel von welchem Produkt du beim Einsatz bestimmter Rohstoffmengen bekommst, rechnest du „rückwärts“.
Dafür multiplizierst du die Matrix mit einem unbekannten Vektor und setzt das Ganze mit dem aktuellen Vektor gleich:
=\begin{pmatrix}0,1&0,6\\0,9&0,4\end{pmatrix}\cdot \begin{pmatrix}a\\b\end{pmatrix}= \begin{pmatrix}20\\30\end{pmatrix}In diesem Fall wären 20 Einheiten des einen und 30 Einheiten des anderen Rohstoffes eingesetzt worden. Die Zahlen a und b stehen für die Mengen der Rohstoffe.
Oder es sind aktuell 20 Jungtiere und 30 ausgewachsene Tiere. Dann stehen a und b für die Anzahlen dieser Tiere im vorangegangenen Jahr.
Spezialbegriffe nach Anleitung anwenden
In manchen Aufgaben wurden neue Fachbegriffe eingeführt. Der Auftrag bestand dann darin, die erklärten Eigenschaften spezieller Matrizen anzuwenden. Ich gebe hier die Definitionen aus den Klausuraufgaben an und zeige, wie sie sich in einer Rechnung anwenden lassen.
(spalten)stochastische Matrix
Betrachtet werden stochastische Matrizen, d. h. quadratische Matrizen, deren Spaltensummen jeweils gleich eins sind und in denen alle Elemente größer als null oder gleich null sind.
Beispiel einer stochastischen 2×2-Matrix:
\begin{pmatrix}a&b\\{1-a}&{1-b}\end{pmatrix}transponieren / orthogonale Matrizen
Eine Matrix wird transponiert, indem sie um eine Diagonale „gekippt“ wird:
M= \begin{pmatrix}a&b&c\\d&e&f\end{pmatrix} \implies M^T=\begin{pmatrix}a&d\\b&e\\c&f\end{pmatrix}Quadratische Matrizen sind orthogonal, wenn Folgendes gilt:
M\cdot M^T=\begin{pmatrix}1&0\\0&1\end{pmatrix}Das musst du nicht im Voraus wissen, es kann allerdings vorkommen, dass diese Fachbegriffe eingeführt werden und du sie dann auf eine quadratische Matrix anwenden sollst, also überprüfen, ob sie orthogonal ist.
In dem Fall kippst du die Matrix und erhältst dadurch die Transponierte. Als letzten Schritt multiplizierst du die Originalmatrix mit der transponierten Matrix. Du hältst dich also an die Anleitung auf dem Arbeitsblatt.
Diagonalmatrix
Eine Diagonalmatrix ist eine quadratische Matrix, die nur Einträge auf der Diagonalen von links oben nach rechts unten hat. Alle anderen Einträge sind Nullen.
Wenn diese Einträge a auf der Diagonalen alle gleich groß sind, bewirkt eine Multiplikation eines Vektors mit dieser Matrix die Multiplikation des Vektors mit dieser Zahl a.
Beispiel:
\begin{pmatrix}1,5&0&0\\0&1,5&0\\0&0&1,5\end{pmatrix}\cdot \begin{pmatrix}E\\L\\K\end{pmatrix}\\\quad\\=\begin{pmatrix}1,5E\\1,5L\\1,5K\end{pmatrix}=1,5\cdot \begin{pmatrix}E\\L\\K\end{pmatrix}In diesem Fall ist a = 1,5. Die Population nimmt bei a>1 zu und bei a<1 ab, aber die prozentualen Verhältnisse der beteiligten Untergruppen, zum Beispiel Eier, Larven und Käfer, bleiben immer gleich.
Grenzmatrix
Die Grenzmatrix ist die Matrix, die ich mit einem beliebigen Zustandsvektor multiplizieren kann, sodass stationäre Vektor herauskommt. Wenn ein Übergangsprozess solch eine Grenzmatrix hat, dann ergibt sie sich im Prinzip dadurch, dass ich die originale Übergangsmatrix so lange immer wieder mit sich selbst multipliziere, bis sich die Einträge nicht mehr verändern.
Bei der Aufgabe, in der eine Grenzmatrix vorkam, musste diese nicht berechnet werden, sondern war gegeben. Die Aufgabe lag darin, die Grenzmatrix zu interpretieren, also zu sagen, wie der stationäre Zustand der Population aussehen würde.
Ein paar Aufgabentypen kamen nur selten vor:
Wie läuft der HMF-Teil im Mathe-Abi möglichst entspannt?
Jetzt hast du einen Überblick, was der HMF-Teil im Mathe-Abi bereit hält. Eine gute fachliche Vorbereitung ist schon die halbe Miete, auch für eine möglichst große innere Entspannung. Was kannst du zusätzlich während und in der Zeit vor der Prüfung tun?
Einer meiner am häufigsten wiederholten Tipps ist: „Mach dir eine Skizze!“ Weil ich davon so überzeugt bin, habe ich dazu einen eigenen Blogartikel geschrieben.
Das Gehirn entspannt, wenn wir zunächst die Informationen aus einer Aufgabe grob auf Papier visualisieren. Viele Dinge, die im Text unverständlich klingen, werden mit Hilfe einer bildlichen Darstellung oft viel offensichtlicher.
Zusätzlich kannst du eine für dich passende Entspannungstechnik lernen. Dazu gibt es online Anleitungen für Meditationen, Atemtechniken, Affirmationen und ähnliche Methoden. Ich selbst habe eine geführte Meditation zur Stärkung der inneren Sicherheit vor Prüfungen geschrieben.
Fragen und Feedback
Diese Artikelreihe liegt mir besonders am Herzen. Und zwar, weil ich aus nächster Nähe sehe, wo die Schwierigkeiten liegen: Darin, die Aufgabenformulierungen überhaupt erst einmal zu verstehen und im generellen Druck, den die ungewisse Prüfungssituation erzeugt. Ich möchte deswegen dazu beitragen, dass möglichst viele Menschen vor ihrer Abiturklausur hilfreiche Informationen erhalten.
Wenn du Fragen hast oder zu meinem Artikel etwas anmerken möchtest, freue ich mich sehr über Rückmeldung. Gerne auch aus anderen Bundesländern 🙂
Und wenn du jemanden in deinem Umfeld hast, der oder die 2024 Mathe-Abi schreiben wird, freue ich mich, wenn du diesen Artikel mit dieser Person teilst.
Auf meinem Blog findest du noch weitere Blogartikel zur Mathematik.


Schreibe einen Kommentar