Was gehört dazu? Welche Aufgaben kommen oft dran?
Bereitest du dich auf die Abiturklausur Stochastik vor? Ich habe die IQB-Aufgaben für dich gesichtet und erzähle dir, was darin vorkam.
Meine Nachhilfeschüler:innen bereiten sich aktuell unter anderem auf das Abitur in Mathematik vor. Ähnlich populär wie die Analysis ist der Teilbereich der Stochastik.
Im Laufe der Evolution war es für uns Menschen leider nicht von Vorteil, lang und breit eine Risikoabschätzung durchzuführen, wenn Gefahr drohte. Vermutlich deshalb scheint für viele von uns dieser Bereich der Oberstufenmathematik besonders mysteriös. Vielleicht geht es dir ja auch so.
Wenn du allerdings besser abschätzen kannst, was auf dich zukommt, ist die Chance größer, dass du bei dieser Prüfung möglichst stressfrei antrittst und damit möglich gut dein gelerntes Wissen zur Verfügung hast.
Dieser Artikel ist zu deiner Information gedacht, aber auch als Abhakliste, was du schon sicher kannst. Und zur Planung, was du noch unbedingt wiederholen solltest. Ich habe Details und Tipps angefügt, die du durch Klick auf den jeweiligen Stichpunkt sichtbar machen kannst. Im Laufe der Zeit werde ich eventuelle neue Informationen noch ergänzen.
In Schleswig-Holstein werden die Abiturklausuren 2024 auf den IQB-Poolaufgaben basieren. Daher fokussiere ich mich mit dieser Artikelserie auf diese öffentlich einsehbaren Übungsaufgaben. Und zwar zunächst auf die Dokumente zum erhöhten Niveau aus den Jahren 2017 bis 2023.
Als Nächstes werde ich über die Vektorrechnung und die Aufgaben im hilfsmittelfreien Teil schreiben. Wenn ich damit fertig bin, füge ich Informationen über das grundlegende Niveau zu.
Wichtig: Natürlich können in zukünftigen Klausuren Aufgaben vorkommen, die von meiner Liste nicht abgedeckt sind.
Abiturklausur StochastikDieser Blogartikel fasst alle meine Beiträge zur Vorbereitung auf das Matheabi zusammen:
Warum sind Klausuren vergangener Jahre interessant?
Viele Abituraufgaben im Fach Mathe wiederholen sich über die Jahre immer wieder. Das gilt für die Stochastik noch mehr als für die Analysis. Daneben gibt es immer Knobelaufgaben aus dem Anforderungsbereich III, für die kreativ über den vorher eingeübten Lernstoff hinaus gedacht werden muss.
Wenn du die häufig vorkommenden Inhalte im Blick hast und diese bei deiner Vorbereitung gut übst, hat das zwei Vorteile:
- Du kannst diese Aufgaben schneller und zuverlässiger erledigen und hast dann mehr Zeit für die kniffeligeren Fragen.
- Du bist von vornherein entspannter. Das steigert deine Erfolgsaussichten ähnlich nachhaltig wie ein solides Faktenwissen.
Was ist mit Stochastik gemeint?
Der Begriff Stochastik kommt vom griechischen στοχαστικὴ τέχνη = „Kunst des Vermutens“. In der Oberstufenmathematik umfasst dies Berechnungen von Wahrscheinlichkeiten, die statistische Auswertung von Daten und die Kombinatorik.
Letztere ist meiner Einschätzung nach besonders wenig mit menschlichen Gehirnen kompatibel. Kombinatorische Aufgaben drehen sich zum Beispiel darum, wie viele Möglichkeiten jemand hat, eine bestimmte Anzahl von Büchern in ein Regal zu stellen. Dabei sehe ich regelmäßig in ungläubige Gesichter 😀
Wie wichtig ein grundsätzliches Verständnis von Stochastik ist, haben wir besonders während der Coronajahre beobachtet. Aus dem Bauch heraus geschätzte Risiken weichen oft von berechneten Wahrscheinlichkeiten ab. Gerade in Krisen ist allerdings möglichst rationales Verhalten möglichst vieler Menschen wünschenswert.
Aufbau einer Abiturklausur Stochastik
In allen Fällen waren Sachaufgaben zu berechnen. Das liegt daran, dass sich für eine Abiturklausur Stochastik auf die Realität bezogene Geschichten anbieten. Währenddessen ist es in der Analysis nicht abwegig, sich mit einer völlig kontextfreien „nackten“ Funktion zu befassen.
Die Geschichten in der Stochastik sind untereinander sehr ähnlich. Meist geht es um Unternehmen, die Produkte oder Dienstleistungen verkaufen oder um ein Glücksspiel. Die häufigen Wiederholungen helfen, sich in die Geschichten hinein zu versetzen.
In ca. 70% der Klausuren gab es im Arbeitsblatt eine durchgehende Hintergrundgeschichte.
Ich habe nach meiner Sichtung die Aufgaben in folgende Kategorien aufgeteilt:
- Wissen aus der Mittelstufe und allgemeine mathematische Fertigkeiten
- Grundsätze der Wahrscheinlichkeitsrechnung
- Baumdiagramme, Vierfeldertafeln, bedingte Wahrscheinlichkeiten und stochastische Unabhängigkeit
- Binomialverteilungen
- Normalverteilungen
- Konfidenz- und Prognoseintervalle
- Hypothesentests
- Kombinatorik
- Fragestellungen aus höheren Anforderungsbereichen
Grundsätzlich sind Hypothesentests, Konfidenz- und Prognoseintervalle, Binomialverteilung und Normalverteilung eigentlich ein großes Thema. In der Abiturklausur Stochastik finden sich allerdings Aufgabentypen mit unterschiedlichen Schwerpunkten. Deswegen habe ich diese Unterthemen separat betrachtet.
Mittelstufenwissen
Abgefragtes Mittelstufenwissen
Dieser Punkt ist mir generell im meinem Unterricht wichtig: In der Mittelstufe lernt ihr eine Reihe von Fakten und Methoden, die ihr in der Oberstufe braucht. Es wird nicht explizit darauf hingewiesen, sondern stillschweigend erwartet, dass ihr das selbst erkennt.
Die erste Methode dieser Art ist die quadratische Gleichung. Zusammen mit binomischen Formeln brauchst du sie zum Beispiel, wenn du es mit einem Baumdiagramm zu tun hast, bei dem du eine unbekannte Trefferwahrscheinlichkeit p ermitteln sollst.
Natürlich kommst du bei den Komplexaufgaben des Matheabiturs ohne pq-Formel aus. Der Taschenrechner löst quadratische Gleichungen schließlich für dich. Nur musst du sie erst einmal als solche erkennen, und nicht irrtümlich davon ausgehen, sie wären nur in der Analysis zu Hause.
Ein zweiter wichtiger Punkt ist die Prozentrechnung. Zusammen mit der Bruchrechnung taucht sie häufig in meinem Unterricht als Schwachstelle auf. Wahrscheinlichkeiten entsprechen relativen Häufigkeiten und werden daher in Prozent angegeben.
Meine Tipps
Ich empfehle dringend:
Schließe deine Gedächtnislücken, was Brüche angeht.
Wiederhole die Umformung von Brüchen, Prozentangaben und Dezimalzahlen ineinander.
Stelle sicher, dass du das wissenschaftliche Zahlenformat kennst, damit dich die Taschenrechneranzeige nicht überrascht.
Was du zum wissenschaftlichen Format wissen solltest
Beispiel: 3,467 · 10-4
Die -4 gibt die Stelle hinter dem Komma an, an der die 3 stehen muss:
0, _ _ _ 3
Die Stellen links der 3 werden mit Nullen aufgefüllt. Die Stellen rechts davon mit der originalen Zahlenfolge „467“:
3,467 · 10-4 = 0,0003467
Negative Exponenten sind relevant für Wahrscheinlichkeiten.
Beispiel 9,1058 · 107
Die 7 gibt an, um wie viele Stellen das Komma nach rechts gerückt werden muss:
91058 _ _ _,
Eventuell entstehende leere Stellen werden mit Nullen gefüllt. Steht das Komma dann rechts am Ende, fällt es weg:
9,1058 · 107 = 91058000
Positive Exponenten sind relevant in der Kombinatorik, weil dort regelmäßig sehr große Zahlen heraus kommen. Als Endergebnis kannst du die Taschenrecheranzeige in diesen Fällen abschreiben. Denke aber daran, die Zehnerpotenz mit anzugeben.
Die restlichen Punkte waren bunt gemischt und tauchten nur in wenigen Jahrgängen jeweils tatsächlich auf. Trotzdem ist es immer eine gute Idee, sie auf dem Schirm zu haben, weil sich damit mancher Sachzusammenhang erst interpretieren lässt:
- Bogenmaß und Winkel (Aufteilung von Glücksrädern)
- Terme und Gleichungen umstellen
- Interpretation von Diagrammen auch mit unbekannten Darstellungsformaten
- Beurteilung der Realitätsnähe eines Modells
Binomische Formeln und die pq-Formel sind in der Formelsammlung zu finden, die dir zur schriftlichen Abiturprüfung ausgehändigt wird. (PDF-Datei) Das Bogenmaß wird dort nur sehr knapp erwähnt, seine Anwendung aber nicht erklärt.
Grundsätze der Wahrscheinlichkeitsrechnung
Grundbegriffe
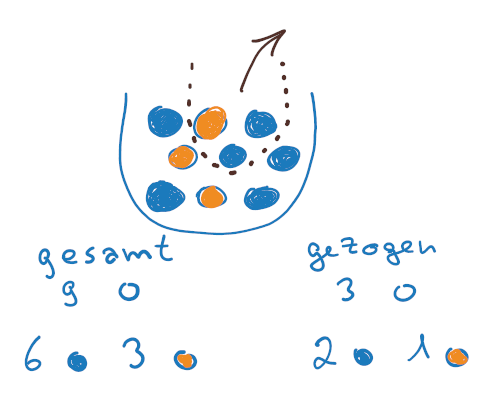
Wahrscheinlichkeiten als Anteile
Dieser Punkt läuft erfahrungsgemäß intuitiv. Oft sollst du aus einer einleitenden Erklärung mit Hilfe einfacher Bruchrechnung Wahrscheinlichkeiten angeben. Dahinter mehr zu vermuten, nur weil dieser Prüfungsteil unter der Überschrift Stochastik läuft, stresst nur unnötig.
Beispiel: In einer Schulklasse sind 20 Kinder. 8 davon tragen eine Brille. Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewähltes Kind eine Brille trägt?
8 : 20 =0,4 bzw. 40 %
Tief durchatmen, mehr steckt hinter dieser Frage nicht 🙂
Wahrscheinlichkeiten aus Winkeln auf einem Glücksrad
Hier hilft dir der Dreisatz: 360° entsprechen 100 %. Ist dein Winkel gegeben, zum Beispiel φ = 72°, dann gehört zu diesem Feld auf dem Glücksrad die Wahrscheinlichkeit 72° : 360° · 100 % = 20 %
Es kommt vor, dass der Winkel zunächst nicht gegeben ist, dann lässt du die Wahrscheinlichkeit als p = φ : 360° stehen.
Manchmal wird der Winkel im Bogenmaß betrachtet, dann gilt: 2π entsprechen 100 %.
Gegenereignis / Gegenwahrscheinlichkeit
Hier ist logisches Denken gefragt. In den IQB-Klausuren habe ich keine klassische 3-mal-mindestens-Aufgabe gefunden. Trotzdem ist es sinnvoll, dir das Gegenteil von „mindestens einmal“ zu merken. Das ist nämlich „Null mal“ und kann Rechnungen drastisch vereinfachen oder mitunter überhaupt erst ermöglichen.
Das generelle Konzept der Gegenwahrscheinlichkeit tauchte mehrfach auf. Wenn ein Ereignis sehr kompliziert zu berechnen ist, lohnt es sich oft, das Gegenereignis zu formulieren. Dessen Wahrscheinlichkeit ziehst du dann von 1 ab.
Häufige Formulierungen in Aufgaben
Logische Formulierungen
Die Abiturklausur Stochastik ist vom Umfang her eher übersichtlich. Nutze deine Zeit, um Texte zweimal zu lesen und wichtiges farbig zu markieren.
Ereignisse können zum Beispiel mit „sowohl als auch“, „weder… noch…“ und „entweder… oder…“ formuliert werden. Eine Skizze hilft dir, daraus Wahrscheinlichkeiten zusammenzusetzen.
Die folgenden Beschreibungen solltest du gut auseinanderhalten:
„mindestens“ -> ≥
„höchstens“ -> ≤
„weniger als“, „unter“ -> <
„mehr als“, „über“ -> >
Für Intervalle, zum Beispiel „mehr als 5 aber höchstens 8“, schreibst du P(5<X ≤8).
In fast 30 % der Fälle tauchte dieser Auftrag auf:
„Geben Sie ein Ereignis an, das…“
Meistens soll das Ereignis zu einem Term passen, der auf der Bernoulli-Formel oder einem Pfad innerhalb eines Baumdiagramms basiert.
Für deine Formulierung entnimmst du Satzbausteine aus der Grundgeschichte und passt n, p und k entsprechend dem gegebenen Term an. Bedenke, dass für k = 0 und k = 1 sich in der Bernoulli-Formel einiges vereinfacht. Ein Beispiel:
{20 \choose 0}\cdot 0,2^0\cdot 0,8^{20}=1\cdot 1\cdot 8^{20}=0,8^{20}\\\quad\\
{20 \choose 1}\cdot 0,2^1\cdot 0,8^{19}=20\cdot 0,2\cdot 8^{19}=4\cdot0,8^{19}In diesem Fall könnte dir der Term 4 · 0,819 + 0,820 präsentiert werden. Aus dem Sachzusammenhang sollte sich ergeben, dass
n = 20 und p =0,2
Der Term beschreibt P(X=0) und P(X=1). Am Ende lautet das Ereignis also zum Beispiel „Von 20 untersuchten Bildschirmen ist höchstens einer defekt.“
Tief durchatmen, es ist nicht so kompliziert, wie es scheinen mag. Und es lohnt sich, diesen Aufgabentyp zu üben
Baumdiagramme / Vierfeldertafeln
Dieser Aufgabentyp taucht besonders häufig und oft am Anfang der Abiturklausur Stochastik auf. Oft soll eine Vierfeldertafel oder ein Baumdiagramm explizit angefertigt oder vervollständigt werden. Manchmal musst du ein gegebenes Baumdiagramm interpretieren.
In einigen Fällen lohnt es sich, ein Baumdiagramm oder eine Vierfeldertafel zu erstellen, ohne dass dies ausdrücklich gefordert ist. Denn beide helfen, eine Textaufgabe kompakt und anschaulich darzustellen. Welches der beiden Formate du wählst, ist dabei eher eine Frage deiner Präferenz.
Folgende Aufgaben fallen in diesen Themenbereich:
Baumdiagramm mit unbekannter Wahrscheinlichkeit p
Beim Zeichnen schreibst du an den entsprechenden Zweig ein p und an den Zweig zum Gegenereignis (1-p). Wenn du die einzelnen Pfade durchmultipliziert und das Ergebnis mit einer gegebenen Wahrscheinlichkeit gleichgesetzt hast, löst du nach p auf.
Dies ist eine Stelle, an der (wie weiter oben angekündigt) eine quadratische Gleichung vorkommt 🙂
Bedingte Wahrscheinlichkeiten
Die Aufgaben fragen nicht explizit nach bedingten Wahrscheinlichkeiten, sondern enthalten häufig Relativsätze oder Konditionalsätze:
- „…, dass ein Bildschirm, der defekt ist, im Test durchfällt“
- „…, dass ein Bildschirm im Test durchfällt, wenn er defekt ist.“
Eine ähnliche Logik enthalten Formulierungen der Art:
- „…, dass ein defekter Bildschirm durchfällt.
In allen Fällen wird bei zwei Eigenschaften nach dem Vorkommen der einen Eigenschaft in der Untergruppe gefragt, die auch die andere Eigenschaft trägt.
Im Baumdiagramm stehen die bedingten Wahrscheinlichkeiten an den unteren Zweigen, wie im folgenden Beispiel:
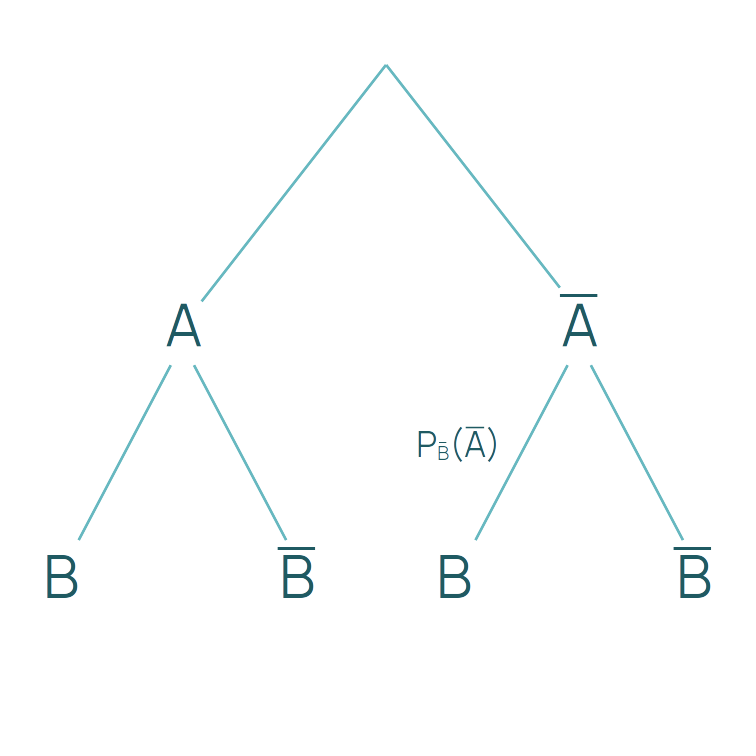
In der Vierfeldertafel kannst du die bedingten Wahrscheinlichkeiten nicht direkt ablesen, sondern musst sie berechnen:
P_A(B)=\frac{P(A\cap B)}{P(A)}Stochastische Unabhängigkeit
Es wurde ausdrücklich der Begriff „abhängig“ beziehungsweise „unabhängig“ verwendet. Berechne die relevanten bedingten Wahrscheinlichkeiten und vergleiche, zum Beispiel:
PA(B) = P(B)
Wenn diese Gleichung stimmt, sind die Eigenschaften A und B unabhängig.
Wahrscheinlichkeit bei einem mehrstufigen Experiment
Bei einem Ereignis der Sorte „Bei dreimaligem Würfeln kommt dreimal eine Sechs heraus“ hilft ein Baumdiagramm und das Befolgen der Pfadregeln.
Binomialverteilungen
Grundsätze der Binomialverteilung
Oft steht über einer Aufgabe aus dem Bereich Verteilungen: „Definieren Sie ihre Zufallsvariable„. Dieser Schritt ist für dich sehr wichtig, weil von einer sauberen Definition abhängt, wie klar du die folgenden Rechenschritte aufbaust.
Manchmal ist die Zufallsvariable schon definiert. Dann empfehle ich, sie farbig zu markieren und die Formulierung zweimal zu lesen.
In den meisten Fällen beginnt die Definition mit „Anzahl der…“. Versetze dich in die Lage der Person aus der Geschichte und überlege dir, wo ihr Interesse liegt und was sie mit einer Strichliste in der Hand zählt. Das sind die sogenannten Treffer.
Die Trefferwahrscheinlichkeit p steht manchmal im Text. Manchmal musst du sie als Anteil berechnen. In anderen Fällen ist die Wahrscheinlichkeit für eine Niete gegeben, diese ziehst du von 1 ab.
Auch wenn du Wahrscheinlichkeiten mit dem Taschenrechner berechnest, solltest du die Bernoulliformel beherrschen und verstanden haben, was passiert, wenn du für k eine 1 oder eine 0 einsetzt. Denn regelmäßig ist die Aufgabe einen gegebenen Bernoulliterm zu interpretieren oder selbst zu einem Sachverhalt den passenden Term anzugeben.
Darf die Binomialverteilung angewendet werden?
Streng genommen ist eine Verteilung nicht binomial, wenn p nicht konstant bleibt, also zum Beispiel nicht zurückgelegt wird. Bei Umfragen werden Personen nicht zweimal befragt. Bei Qualitätstests werden geöffnete Produkte entsorgt und nicht in den Produktstrom zurück gelegt und dann eventuell ein weiteres Mal getestet.
In diesen Fällen kann eine Verteilung als näherungsweise binomialverteilt betrachtet werden, wenn die betrachtete Stichprobe klein ist bei einer großen Grundgesamtheit.
Trotzdem kann bei Sachzusammenhängen mit Menschen ein entscheidender Faktor sein, dass sie in Kleingruppen antreten. Wenn zum Beispiel die Mutter entscheidet, doch nicht in den Freizeitpark zu gehen, bleiben die Kinder auch zu Hause. Die Wahrscheinlichkeit für ihren Freizeitparkbesuch sinkt damit abhängig von der Mutter auf Null.
Rechnen mit der Bernoulliformel
Bernoulli bei k = 1 und k = 0
Für k wird gerne einer dieser Werte gewählt, weil sich dadurch einiges vereinfacht:
\footnotesize {P(k=1)={n \choose 1}\cdot p^1\cdot (1-p)^{(n-1)}=n\cdot p\cdot(1-p)^{(n-1)}}Mit zum Beispiel n = 20 und p = 0,2 wird daraus 4 · 0,819
\footnotesize {P(k=0)={n \choose 0}\cdot p^0\cdot (1-p)^{n)}=(1-p)^{n}}Mit zum Beispiel n = 20 und p = 0,2 wird daraus 0,820
P für Ereignisse berechnen
Wichtig ist, dass du aus dem Text den korrekten Term abliest. „Die Wahrscheinlichkeit für über 15 Treffer“ bedeutet zum Beispiel P(X>15)
Ich empfehle, vorher sicherzustellen, dass du zuverlässig weißt, wie du diese Wahrscheinlichkeiten mit dem Taschenrechner berechnest.
Es war häufig zu berechnen, mit welcher Wahrscheinlichkeit etwas mindestens, höchstens oder zwischen zwei Werten eintrifft. Eine Angabe der Art „genau 20 mal“ kam allerdings auch immer wieder vor.
„X weicht um 0,5 · σ von µ ab“ / „X weicht um 15 % von µ ab“
In diesem Fall berechnest du µ und gegebenenfalls σ:
\mu=n\cdot p \quad\quad\quad \sigma=\sqrt{n\cdot p\cdot(1-p)}Dann addierst du den geforderten Wert einmal zu µ dazu und ziehst ihn einmal ab. Damit hast du deine Werte für das linke und das rechte k und verfährst dann wie im Punkt „P für Ereignisse berechnen“.
Durch Probieren n oder p oder k ermitteln
Auch wenn es nicht explizit in der Aufgabe steht: Wenn zwei der drei Größen n, p und k gegeben sind und eine bestimmte Wahrscheinlichkeit P gefordert ist, bleibt dir nichts übrig, als im Taschenrechner eine der Größen so lange zu variieren, bis sich das gesuchte P ergibt.
Zur nachvollziehbaren Dokumentation schreibst du am besten eine Tabelle mit den verschiedenen Ergebnissen, die du auf dem Weg zur Lösung bekommen hast.
Besondere Aufgabentypen
Dreimal mindestens
In den alten Stochastik-Klausuren aus Schleswig-Holstein kam dieser Aufgabentyp häufig vor. Zwischen 2017 und 2023 war in den IQB-Klausuren nur einmal nach einer Mindestzahl an Versuchen n gefragt. Weil die Trefferzahl mindestens 3 sein sollte, war der Lösungsweg das Ausprobieren.
Weil die klassische „Dreimal mindestens“-Aufgabe mit P(X≥1) so „elegant“ ist , gehe ich davon aus, dass sie in Zukunft auch in den länderübergreifenden Abiturklausuren eine Rolle spielen wird.
Bis ich selbst eine Erklärung geschrieben habe, verweise ich für den immer gleichen Lösungsweg auf dieses Video.
Ineinander verschachtelte Binomialverteilungen
Zwei Bernoulliexperimente können ineinander verschachtelt sein. Ein Beispiel:
Eine Kiste mit 12 Saftflaschen wird akzeptiert, wenn mindestens 10 Flaschen das vorgegebene Volumen Saft enthalten. Die Firma befüllt erfahrungsgemäß 2 % der Flaschen nicht ordentlich. Ein Unternehmen kauft 100 Kisten.
Wie groß ist die Wahrscheinlichkeit, dass 100 von 100 Kisten in Ordnung sind?
- Zufallsgröße Y: Anzahl der ordentlich befüllten Flaschen in einer Kiste
nY = 12 kY = 10
pY = P(„Flasche ist ordentlich befüllt“)= 1 – 0,02 = 0,98 - Zufallsgröße Z: Anzahl der akzeptierten Kisten
nZ = 100 kz = 100
pz = P(„Kiste wird akzeptiert“)
Die Wahrscheinlichkeit, dass eine Kiste akzeptiert wird (pZ) ist P(Y≥10). Es muss also zunächst die eine Teilaufgabe erledigt und dann deren Ergebnis bei der zweiten Teilaufgabe eingesetzt werden.
Mit nY = 12 und pY = 0,98 ist P(Y≥10) ≈ 0,9985 = pZ
Mit nZ = 12 und pZ = 0,9985 ist P(Z=100) ≈ 0,8606
Grundsätzlich brauchst du für diese Aufgabe keine unbekannte oder komplizierte Rechenmethode. Du musst nur logisch denkend vorgehen, deine Variablen sauber definieren und dann in Ruhe deine Rechenschritte abarbeiten.
Anwendung auf Sachzusammenhang
Balkendiagramm einer Binomialverteilung zuordnen
Der Auftrag kann lauten „Begründen Sie, warum dieses Diagramm nicht die beschriebene Binomialverteilung darstellen kann“.
Für eine Antwort berechnest du µ, den Wert für P(X=µ) und siehst dir auch die Symmetrie des Balkendiagramms an. Bei einem p von 0,5 sind die Balken symmetrisch mit µ in der Mitte. Bei größeren Werten für p ist der Verlauf nach rechts „gekippt“, bei kleineren entsprechend nach links.
Für die Gleichung und das Diagramm sollten die Werte übereinstimmen, damit du sie einander zuordnen kannst.
Was außerdem manchmal abweicht, ist das n. Wenn zum Beispiel in der Binomialverteilung ein Wert von 20 vorgesehen ist, im Diagramm aber bei X = 25 noch ein positiver Balken erscheint, passt das nicht zusammen.
Ausdruck der Art P(X=20)=0,2 im Sachzusammenhang interpretieren
Dahinter steckt wirklich nicht mehr, als dass du diese Gleichung in einen Satz umschreibst. In diesem Fall also:
„Die Wahrscheinlichkeit, dass genau 20mal getroffen wird, liegt bei 20 %“
Normalverteilungen
Grundsätze Normalverteilung
Auch bei Normalverteilungen ist es entscheidend, dass du im Blick hast, was deine Zufallsgröße überhaupt ist. Normalverteilungen sind streng genommen für Zufallsgrößen definiert, die stetig sind (Beispiel Füllvolumen). Binomialverteilungen gelten dagegen für ganzzahlige Zufallsgrößen (Beispiel Personenzahl).
Weil du Wahrscheinlichkeiten sowieso mit dem Taschenrechner ermittelst, spart die Normalverteilung kaum Aufwand. Es kann trotzdem vorkommen, dass du mit der Laplace-Bedingung begründen sollst, warum du eine Binomialverteilung näherungsweise als normalverteilt betrachten darfst.
Mit µ und σ rechnen
µ und σ berechnen, Laplace-Bedingung
\mu=n\cdot p \quad\quad\quad \sigma=\sqrt{n\cdot p\cdot(1-p)}Wenn σ größer als 3 ist, ist die Verwendung der Normalverteilung zulässig.
Begriff Dichtefunktion
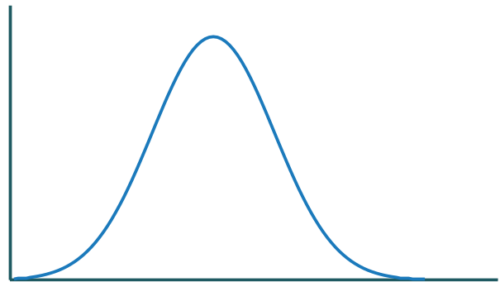
In manchen Aufgabe fällt der Begriff „Dichtefunktion“. Dies ist die Funktion, die einem Wert einer Zufallsgröße eine Wahrscheinlichkeit zuordnet. Im Zusammenhang mit der Normalverteilung kennst du sie als Glockenkurve.
Von den Größen P, µ, σ und X sind drei gegeben, die vierte ist gesucht.
Je nach Taschenrechner hast du unterschiedliche Eingabemethoden, um aus µ, σ und X die gesuchte Wahrscheinlichkeit P zu berechnen.
Es kommt auch vor, dass P vorgegeben ist. Dann sind von den anderen drei Größen auch jeweils zwei gegeben und du musst die letzte Größe im Taschenrechner so lange variieren, bis das gewünschte P herauskommt.
µ und σ aus gegebener Dichtefunktion entnehmen
Die Funktion hat diese Form:
\Large{\Phi(x)=\frac{1}{\sigma\cdot \sqrt{2\pi}}\cdot e^{-\frac{1}{2}\cdot ( \frac{x-\mu}{\sigma})^2}}In einer gegebenen Funktion musst du nur die Zahlen identifizieren, die an den Positionen für σ und µ stehen. Die gute Nachricht ist: Du musst diese Formel nicht auswendig wissen, denn sie steht in der IQB-Formelsammlung.
Interpretation des Graphen
Dichtefunktion skizzieren, Auswirkung der Veränderung von µ und σ
Das µ gibt die x-Koordinate des Maximums an, oder mit anderen Worten den Erwartungswert. Die Standardabweichung σ ist ein Maß dafür, wie hoch und breit die Glockenkurve ist.
Wird µ größer, rückt die Kurve nach rechts.
Wird σ größer, wird die Kurve breiter und flacher.
Den Effekt kannst du auf dieser Geogebra-Unterseite mit Schieberegler zur Glockenkurve ausprobieren.
Diagramm einer Normalverteilung geometrisch interpretieren
Die Fläche zwischen der Glockenkurve und der x-Achse entspricht der Wahrscheinlichkeit, die zu dem jeweiligen Intervall gehört.
Die komplette Fläche ist 1, was einer Wahrscheinlichkeit von 100% entspricht. Irgendetwas muss einfach passieren 🙂
In manchen Aufgaben ist ein Diagramm gegeben, in dem du die zu einer Geschichte passende Fläche einfärben und abschätzen sollst.
Dichtefunktion mit der Zeit auf der x-Achse
Bei Binomialverteilungen ist die Zufallsgröße meistrens etwas, was gezählt wird. Andererseits war in manchen Aufgaben zu einer Normalverteilung auf der x-Achse die Zeit eingetragen.
Mein Tipp: Lass dich davon nicht verunsichern. Du kannst trotzdem µ, σ und X normal verwenden. Dann ist einfach µ die Zeit, zu der am wahrscheinlichsten etwas passiert.
σ-Umgebungen
Aufgaben zu σ-Umgebungen waren in den betrachteten Klausuren nicht vertreten. Bis ich selbst eine Erklärung geschrieben habe, kannst du dich mit diesem Video vorbereiten.
Die Tabelle mit benötigten Faktoren für verschiedene Umgebungen steht in der IQB-Formelsammlung. Daher ist es nicht ausgeschlossen, dass eine Frage aus diesem Bereich in Zukunft drankommt.
Hypothesentests
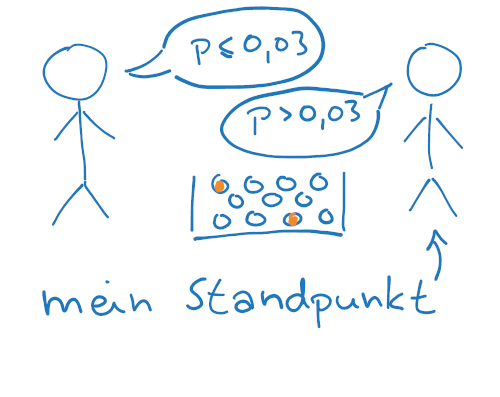
Grundsätze der Hypothesentests
Hypothesentests basieren meistens auf einer Konfliktsituation. Zwei Personen behaupten unterschiedliche Dinge und mit Hilfe einer Stichprobe wollen sie entscheiden, welcher Standpunkt wahrscheinlich richtig ist.
Wichtig: Wir finden dabei nicht die absolute Wahrheit heraus!
Wir versuchen nur das Risiko, die falsche Entscheidung zu treffen, möglichst klein zu halten.
Hypothesen aufstellen und Entscheidungsregeln finden
Test rechts, links, beidseitig oder alternativ
In 50 % der Klausuren war ein Hypothesentest verlangt, die meisten darunter rechtsseitig, der Rest linksseitig. Die Nullhypothese H0 war jeweils gegeben. Sollte sie einmal nicht gegeben sein, ist meistens dein Standpunkt (beziehungsweise der Standpunkt der Person, die den Test durchführt) die H1.
An der H1 liest du ab, auf welcher Seite du testest.
H_1: p<0,5
Das Zeichen sieht aus wie ein Pfeil nach links: linksseitiger Test.
H_1: p\neq 0,5
Das durchgestrichene Gleichheitszeichen weist nach beiden Seiten: beidseitiger Test.
H_1: p>0,5
Das Zeichen sieht aus wie ein Pfeil nach rechts: rechtsseitiger Test.
H_1: p=0,4\\ H_2: p=0,6
Es gibt zwei festgelegte Alternativwerte für p: Alternativtest.
Nullhypothese begründen
In mehreren Fällen sollte erläutert werden, aus welcher Motivation heraus die Nullhypothese gewählt wurde. Die Antwort ergibt sich daraus, dass ein Betrieb verschiedene Risiken hat, je nachdem welche Hypothese verworfen wird.
Zum Beispiel führen Lieferungen mit zu vielen fehlerhaften Teilen zu verärgerten Kund*innen und Reklamationskosten. Auf der anderen Seite führen übermäßig gründliche Qualitätstests zu höheren Betriebskosten. Hier muss die Firma eine Priorität festlegen, an welche Stelle sie sparen will, beziehungsweise welchen Schaden sie vermeiden will.
Entscheidungsregel
Mit deinem Taschenrechner erzeugst du eine Tabelle, aus der sich das letzte k ergibt, das noch im Ablehnungsbereich der H0 ist. Je nachdem, ob du links oder rechts testest, ist das das kleinste oder das größte k.
Auf dieser Basis formulierst du deine Entscheidungsregel:
„Die Nullhypothese wird verworfen, wenn unter [n] [was auch immer gezählt wird] höchstens/mindestens [k] [Beschreibung des jeweiligen Treffers] sind“.
Für einen beidseitigen Test musst du den rechten und den linken Ablehnungsbereich beschreiben.
Mit Fehlern rechnen
Fehler zweiter Art im Sachzusammenhang beschreiben / berechnen
Ein Fehler zweiter Art (auch als β-Fehler bezeichnet) bedeutet, dass wir H0 nicht verwerfen, obwohl H1 gilt. Diesen Fehler kannst du nur berechnen, wenn eine alternative Wahrscheinlichkeit p1 gegeben ist.
Zur Veranschaulichung empfehle ich diese Geogebra-Unterseite. Die Definition des Fehlers zweiter Art steht außerdem auch in der Formelsammlung.
Betriebliche Risikoabschätzung
Mit Hilfe des Erwartungswertes kann für einen Betrieb berechnet werden, von welchen Kosten bei einer vorgegebenen Entscheidung ausgegangen werden muss. Auf dieser Basis sollst du dann erläutern, welche Entscheidung du an Stelle der Verantwortlichen in einer vorgegebenen Frage treffen würdest.
Aus Fehler zweiter Art auf Alternativ-p schließen
Ist der Fehler zweiter Art bekannt, kann durch Ausprobieren mit dem Taschenrechner die alternative Trefferwahrscheinlichkeit ermittelt werden. Dabei wird die Anzahl von Nachkommastellen vorgegeben.
Konfidenz- und Prognoseintervalle
Hintergrund
Ich habe bisher nicht beobachtet, dass meine Schüler*innen im Schulunterricht in Schleswig-Holstein ausdrücklich etwas über dieses Thema hören, in Hamburg wird es behandelt, allerdings nicht sehr ausführlich.
Daran gemessen sind diese Intervalle für die Abiturklausur Stochastik auf IQB-Basis relevant. Die benötigten Formeln stehen in der IQB-Formelsammlung mit einer relativ umfassenden Anleitung, was du jeweils machen musst.
Diese Geogebra-Unterseite veranschaulicht das Wichtigste mit Schiebereglern für alle beteiligten Größen. Dieses Video erklärt die Unterschiede zwischen Sigma-, Prognose- und Konfidenzintervall.
Wir können die „wahre“ relative Häufigkeit eines Merkmals oft nicht messen, sondern nur schätzen. Bei einer Urne mit 15 blauen und 5 roten Kugeln ist das kein Problem. Bei der Frage, wie viele Menschen gerne Kaffee trinken, ist es schon nicht mehr möglich. Wie gut unsere Schätzung ist, drücken wir mit dem Konfidenzintervall aus.
Rechnen mit Konfidenzintervallen
Intervall ermitteln
Häufig stehen die relevanten Formeln im Aufgabentext und du musst nur noch p und n einsetzen. Das ist eine Gelegenheit, bei der es sich auszahlt, Ruhe zu bewahren und für ein einfaches Eintippen in den Taschenrechner eventuell entscheidende Klausurpunkte mitzunehmen.
Bei anderen Aufgabenstellungen mussten die Werte für die relative Häufigkeit hmin und hmax, beziehungsweise für pmin und pmax aus einem Diagramm abgelesen werden.
Gegebene Größen anhand des Konfidenzintervalls beurteilen
Bei dieser Art Aufgabe wird im Allgemeinen danach gefragt, ob ein Testergebnis mit einem Konfidenzintervall „verträglich“ ist oder „damit im Einklang“ steht.
Mit den bekannten Werten berechnest du das Konfidenz- beziehungsweise Prognoseintervall und überprüfst, ob das Testergebnis darin liegt.
Zusammenhang zwischen n und der Breite des Intervalls
Je größer die Stichprobe, umso schmaler werden Konfidenz- und Prognoseintervall. In einer Klausur war die Frage, warum das so ist, und in welchem Umfang.
Die Antwort liegt in der Formel. Die Wurzel aus der Stichprobengröße steht im Nenner, deswegen bewirkt ein vervierfachtes n eine Halbierung der Intervallbreite.
Aus gegebenem Intervall auf n schließen
Wenn h und p gegeben sind, findest du mit Hilfe der Formeln durch Ausprobieren das dazu passende n heraus.
Erwartungswert bei willkürlichen Verteilungen
Der Erwartungswert E(X), der sich aus einer Tabelle mit einer willkürlich zugeordneten Verteilung ergibt, war in 40 % der Übungsklausuren gefordert. Diese Tabellen stehen meist im Zusammenhang mit Gewinnspielen, bei denen unterschiedliche Geldbeträge mit unterschiedlich hoher Wahrscheinlichkeit zu gewinnen sind.
Erwartungswert berechnen
E(X) ergibt sich, wenn du alle Werte, die die Zufallsgröße X annehmen kann mit der jeweils dazu gehörenden Wahrscheinlichkeit multiplizierst und dann alle Ergebnisse zusammen addierst.
Ich empfehle, falls nicht schon gegeben, eine Tabelle aufzustellen und die einzelnen Summanden dann unter die jeweiligen Spalten zu schreiben:
| X | 10 | 20 | – 8 |
| P(X) | 0,1 | 0,05 | 0,85 |
| X · P(X) | 1 | 1 | – 6,8 |
Wäre dies ein Spiel, wäre der Erwartungswert für den Gewinn
E(X) = 1 € + 1 € – 6,80 € = – 4,80 €
Du kannst also davon ausgehen, bei jedem Spiel durchschnittlich 4,80 € zu verlieren.
faires Spiel
Bei einem fairen Spiel ist der Erwartungswert für die Auszahlung gleich dem Wetteinsatz. Der durchschnittliche Gewinn ist also Null.
Aus gegebenem Erwartungswert den Geldbetrag einer Gewinnkategorie berechnen
Wenn der Erwartungswert gegeben und in der Tabelle für ein Spiel ein Gewinnbetrag gesucht ist, schreibst du in der jeweiligen Zelle anstelle einer Zahl die Variable x.
Beispiel: Bei diesem Spiel ist der Erwartungswert gegeben mit:
E(X) =1,50 €
| X | 10 | 20 | x |
| P(X) | 0,15 | 0,05 | 0,80 |
| X · P(X) | 1,5 | 1 | 0,80 · x |
E(X) = 2,50 € + 0,85 · x = 1,50 €
Diese Gleichung löst du dann nach x auf: x = – 1,25 €
Kombinatorik
In den bisher veröffentlichten IQB-Klausuren waren die Kombinatorikaufgaben auf einem einfachen Niveau. Es saßen also nicht Personen im Kreis und es gab keine Frage nach zum Beispiel vierstelligen geraden Zahlen über 540. Das bedeutet natürlich nicht, dass nicht in zukünftigen Klausuren komplexere Betrachtungen drankommen könnten.
Diese beiden Punkte kamen mehrfach vor:
Grundformeln der Kombinatorik anwenden
Frage dich, ob bei dem Zählverfahren zurückgelegt wird oder nicht, ob die Reihenfolge wichtig ist oder nicht, und eventuell ob alles verteilt wird oder nicht.
n: Aus wie vielen Optionen kann ich für jede Ziehung wählen?
k: Wie oft ziehe ich?
Der größte Teil der Geschichten lässt sich auf folgende Grundmuster zurückführen:
Prinzip Zahlenschloss (mit Zurücklegen, mit Beachtung der Reihenfolge)
\footnotesize n^k
Prinzip Klassenphoto (ohne Zurücklegen, mit Beachtung der Reihenfolge, alle Kinder kommen mit auf das Photo)
\footnotesize n!
Prinzip Siegertreppchen (ohne Zurücklegen, mit Beachtung der Reihenfolge, nur ein Teil der Teilnehmenden kommen auf das Treppchen)
\footnotesize\frac{n!}{(n-k)!}Prinzip Blumenstrauß, bei dem n Blumen zusammen gebunden werden, wobei aus k Farben gewählt werden kann.
\footnotesize{{n+k-1} \choose {k-1}}Prinzip Weihnachtsmann, der mit einem Griff aus seinem Sack drei Geschenke für ein Kind zieht (ohne Zurücklegen, Reihenfolge egal, Hauptsache Geschenke 😉)
\footnotesize {n \choose k}Stelle sicher, dass du weißt, wie du die Zahlen für das Weihnachtsmannprinzip (offiziell: den Binomialkoeffizienten) in deinen Taschenrechner eingibst.
Im zweiten Schritt Wahrscheinlichkeiten berechnen
Wenn du schon eine Anzahl von Möglichkeiten berechnen sollst, schließt sich oft die Frage nach einer Wahrscheinlichkeit an. Dafür gilt:
P=\frac {\text {Anzahl der günstigen Möglichkeiten}}{\text{Anzahl aller Möglichkeiten}}Beide Anzahlen berechnest du mit einem Ansatz aus der Kombinatorik. Oft helfen Skizzen erheblich weiter.
Aufgaben aus höheren Anforderungsbereichen
Neben den Konfidenzintervallen ist mir als besondere Herausforderung nur eins aufgefallen: Die Interpretation unbekannter Diagrammformate. Unter dem Druck der Prüfungssituation kann es schwieriger sein, aus den gewohnten Denkschienen abzubiegen. Ich rate dazu, immer erst einmal zu unterstellen, dass nichts so schlimm gemeint ist, wie es eventuell wirkt 🙂
Wie gehe ich entspannt in die Abiturklausur Stochastik?
Jetzt hast du einen Überblick, was dich in der Abiturklausur Stochastik erwartet. Eine gute fachliche Vorbereitung ist schon die halbe Miete, auch für eine möglichst große innere Entspannung. Was kannst du zusätzlich während und in der Zeit vor der Prüfung tun?
Einer meiner am häufigsten wiederholten Tipps ist: „Mach dir eine Skizze!“ Weil ich davon so überzeugt bin, habe ich dazu einen eigenen Blogartikel geschrieben. Ich bin überzeugt davon, dass es das Gehirn entspannt, wenn wir zunächst die Informationen aus einer Aufgabe grob auf Papier visualisieren.
Viele Dinge, die im Text unverständlich klingen, werden mit Hilfe einer bildlichen Darstellung oft viel offensichtlicher. Das betrifft ganz besonders Kombinatorikaufgaben.
Außerdem kannst du dir eine für dich passende Entspannungstechnik aneignen. Dazu gibt es online Anleitungen für Meditationen, Atemtechniken, Affirmationen und ähnliche Methoden. Ich selbst habe eine geführte Meditation zur Stärkung der inneren Sicherheit vor Prüfungen geschrieben.
Fragen und Feedback
Diese Artikelreihe liegt mir besonders am Herzen. Und zwar, weil ich aus nächster Nähe sehe, wo die Schwierigkeiten liegen: Darin, die Aufgabenformulierungen überhaupt erst einmal zu verstehen und im generellen Druck, den die ungewisse Prüfungssituation erzeugt. Ich möchte deswegen dazu beitragen, dass möglichst viele Menschen vor ihrer Abiturklausur hilfreiche Informationen erhalten.
Wenn du Fragen zur Abiturklausur Stochastik hast oder zu meinem Artikel etwas anmerken möchtest, freue ich mich sehr über Rückmeldung. Gerne auch aus anderen Bundesländern 🙂
Und wenn du jemanden in deinem Umfeld hast, der oder die 2024 Matheabi schreiben wird, freue ich mich, wenn du diesen Artikel mit dieser Person teilst.
Alle Blogartikel zur Mathematik findest du hier.



Schreibe einen Kommentar